Die waagerechte Richtung
| Publikation: | 26.10.2007 |
| Lernstufe: | 3 |
| Dauer: | 3 Unterrichtsstunden à 30 bis 45 Min. (im Klassenraum) |
| Material: |
Für die Klasse: Experiment mit den mit Wasser gefüllten Gefäßen:
Für jede Gruppe von 2 Schülern: Anfertigung von Wasserwaagen:
|
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Voruntersuchung
Um den Begriff "waagerecht" zu definieren, zählen Kinder im Allgemeinen diverse Dinge aus dem Alltag auf, wie z. B. den Fußboden: "Der ist immer ganz eben, und wenn er sich ein bisschen wölbt, spürt man das sofort"; oder die Tischplatte, "die ist auch ganz eben, doch wenn sie etwas geneigt ist, kommt eine Kugel darauf ins Rollen und fällt auf den Boden". Waagerecht ist für sie also gleichbedeutend mit Stabilität, so wie sie senkrecht mit Gleichgewicht in Verbindung bringen. Dies erklärt vielleicht auch, warum sie nicht an (unbewegtes) Wasser denken, das für sie dem Wesen nach instabil ist. Lassen Sie sie eine Flüssigkeit in einem Behälter zeichnen: Viele werden die Wasseroberfläche wellenförmig malen. Und bei einer Flasche, aus der Wasser in ein Glas gegossen wird, werden sie den Wasserspiegel schräg zeichnen.
Versuch
Um zu zeigen, dass die freie Oberfläche einer Flüssigkeit waagerecht ist, wird ein kleiner Versuch durchgeführt, für den die Schüler sich zu Gruppen von 3-5 zusammentun.
Jede Gruppe schneidet aus einem großen weißen Blatt Papier eine beliebige unregelmäßige Form aus und befestigt diese an der Wand oder an der Tafel. Etwa ein Dutzend verschiedene Gefäße aus durchsichtigem (oder durchscheinendem) Kunststoff werden auf einen Tisch in der Mitte des Raums gestellt. Man kann z. B. Tiefkühl-, Nahrungsmittel- oder Reinigungsmittelbehälter (die sauber sein müssen) mit quadratischer, rechteckiger oder länglicher Form verwenden. Sie werden bis zu einem Viertel mit leicht gefärbtem Wasser gefüllt.
In jeder Gruppe hält ein Schüler ein Gefäß leicht schräg und ohne zu wackeln gegen eines der weißen Blätter, während ein anderer Schüler den Umriss des Gefäßes zeichnet. Sobald das Wasser zur Ruhe gekommen ist, markiert er auf jeder Seite des Gefäßes den Wasserstand. Das Gleiche wird mit verschiedenen und unterschiedlich geneigten Gefäßen durchgeführt. Danach werden für jeden Gefäßumriss die beiden Wasserstandmarkierungen miteinander verbunden. Manche Schüler benutzen dafür automatisch ein Lineal (Abb. 2).
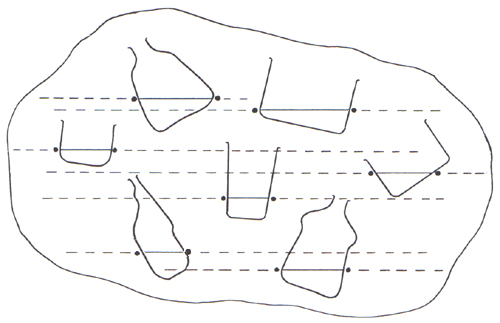
Abb. 2: Umrisse der Gefäße und Markierungen der Waseroberflächen
Die Kinder stellen fest, "dass alle Striche ganz eben sind." Wie lässt sich das überprüfen? "Man kann die Linien mit einem langen Lineal nach beiden Seiten verlängern, um es besser sehen zu können". Vielleicht bemerkt einer: "Das ergibt parallele Linien; das können wir nachprüfen, so wie wir es vor einigen Tagen mit unseren Pauspapieren getan haben." (siehe Abb. 6 der Projektphase 1). Und ein/e andere/r bemerkt: "Die sind richtig eben wie der Boden. Die sind waagerecht." Wie kann man das überprüfen?
Schüler, deren Eltern gern basteln und werkeln, werden sicher die Wasserwaage nennen und vorschlagen, eine mit in die Klasse zu bringen. Damit kann man nachweisen, dass die auf die weißen Blätter gezeichneten Linien, die die Wasserspiegel in den Gefäßen wiedergeben, waagerecht sind (Abb. 3).
Achten Sie darauf, dass die Blätter genau so hängen bleiben, wie sie jetzt hängen, damit die Schüler gleich den rechten Winkel entdecken können (siehe weiter unten).
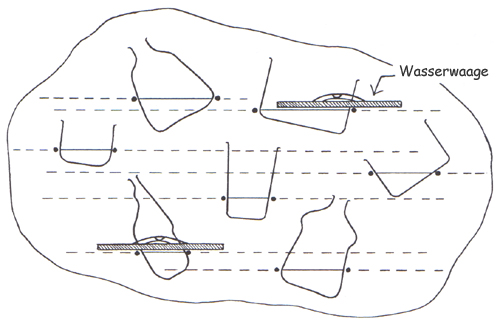
Abb. 3: Mit einer Wasserwaage überprüfen, dass die Wasseroberflächen waagerecht sind
Anfertigung und Benutzung von Wasserwaagen
Mit 20 cm langen und 40 mm breiten Abdeckleistenstücken, Ampullen mit Kochsalzlösung und Klebeband lassen sich rasch einfache aber sehr brauchbare Wasserwaagen anfertigen. Die Ampulle wird flach in die Mulde der Abdeckleiste gelegt und mit Klebeband an beiden Enden befestigt. Dann testet man das Ganze auf einer Fläche, die sich bei der Prüfung mit einer "richtigen" Wasserwaage als waagerecht erwiesen hat, um bei Bedarf die Position der Ampulle auf der Leiste mit Hilfe von "Papierkeilchen" so zu korrigieren, dass die Luftblase in der Mitte der Ampulle stehen bleibt. Die Schüler werden sehen, dass es nicht notwendig ist (wie bei den handelsüblichen Geräten) beiderseits Markierungsstriche anzubringen, denn schon bei der geringsten Neigung verschiebt sich die Blase an eines der Enden der Ampulle.
Die Schüler probieren nun ihre Wasserwaagen an Tischen, Bänken, Regalen usw. aus. Doch oft begnügen sie sich damit, sie nur in einer einzigen Richtung hinzulegen, meistens parallel zu einer Kante. Stellen Sie sie dann vor folgende Herausforderung: Heben Sie eines der Tischbeine leicht an (indem Sie z. B. ein Buch unterlegen); die Schüler sollen die Blase auch in diesem Fall wieder in die Mitte bringen. Nach einigen Versuchen wird ihnen dies gelingen, und sie werden begreifen, dass man die Wasserwaage bei einem Gegenstand mindestens in zwei verschiedenen Richtungen auflegen muss, wenn man überprüfen möchte, ob er waagerecht ist.
Auf experimentellem Weg den rechten Winkel entdecken
Lassen Sie die Schüler jetzt ihre Senklote an die Umrisse der noch an den Wänden und der Tafel hängenden Zeichnungen der Gefäße halten und fragen Sie sie, ob ihnen etwas Interessantes auffällt. "Die Schnur des Senklotes bildet mit der Linie, die die Wasseroberfläche darstellt, ein Pluszeichen (+)."
Geben Sie jeder Gruppe ein kleines buntes Blatt Papier und fragen Sie, ob man dieses nicht vielleicht in die "Kreuzung" einfügen könnte. Die Schüler erkennen sofort, dass das Blatt nicht nur in jede der vier "Ecken" (Winkel) passt, sondern dass es auch jedes Mal passt, wenn man es um die Waagrechte oder Senkrechte klappt (Abb. 4). "Man könnte in die Kreuzung auch vier Zeichendreiecke von der Art, wie mein großer Bruder eins besitzt, einsetzen. Damit zeichnet er rechte Winkel, wie wir sie auch in unserem Fragebogen finden mussten."
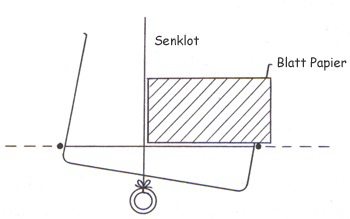
Abb. 4: An der "Kreuzung" von Waagrechten (Wasseroberfläche) und Senkrechten (Senklot) entstehen rechte Winkel.
Die Schüler werden ihre Umgebung nach Gegenständen mit rechten Winkeln absuchen und sie werden viele finden. Sie können sich auch darin üben, mit dem Zeichendreieck rechte Winkel zu zeichnen, wobei sie feststellen werden, dass man das Zeichendreieck nicht braucht, wenn man Millimeter- oder kariertes Papier verwendet (das gilt natürlich nur für den Fall, dass eine Seite des rechten Winkels sich mit einer Linie deckt oder parallel zu ihr ist).
Nachdem die Schüler entdeckt haben, dass das, was gerade ist, senkrecht, und das, was eben ist, waagerecht ist, und dass die Kreuzung beider Richtungen einen rechten Winkel ergibt, wird ihnen bewusst, dass die Gnomone genau senkrecht auf ihren genau waagrechten Unterlagen befestigt werden müssen, um zuverlässige Messungen durchführen zu können.
Letzte Aktualisierung: 29.11.2023






