Den Erdumfang mit Hilfe der Messungen anderer Schulen bestimmen
| Publikation: | 27.10.2007 |
| Lernstufe: | 3 |
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Vorbemerkung
Wenn genügend Zeit vorhanden ist, sollten Sie sich mit den Kindern unbedingt die fakultativen Aktivitäten über Breiten- und Längengrade auf der Erdkugel ansehen und die von Ihren Schülern gemessenen Werte für den Winkel mit denjenigen anderer Schulen vergleichen. Wenn dafür die Zeit nicht reicht, können sich die Kinder mit Hilfe eines Globus und einer Weltkarte mit den genannten Begriffen vertraut machen (fakultative Unterrichtseinheit: "Sich auf der Erde zurechtfinden").
Einen Partner wählen
Wir zählen zunächst die Voraussetzungen auf, die zu erfüllen sind, wenn diese letzte Etappe ein Erfolg werden soll.
Die Kinder müssen die Schattenlänge ihres Gnomons gemessen haben – und zwar genau am Sonnenmittag (mit einer Toleranz von höchstens 10 Minuten) – und aus dieser Messung die genaue Größe des Winkels der Sonnenstrahlen mit der Senkrechten ihres Standortes abgeleitet haben.
Sie müssen ihre(n) Winkelmesswert(e) auf der bereitgestellten Übersicht eingetragen haben, damit die anderen am Projekt beteiligten Klassen diese Messwerte verwenden können.
Anschließend müssen sie eine Partnerschule wählen, die ihre eigene Messung am Sonnenmittag des gleichen Tages gemacht hat (im Juni ist eine Abweichung von zwei Tagen zulässig). Die Partnerschule muss mindestens 3 oder 4 Grad weiter südlich oder nördlich vom Breitengrad ihrer eigenen Schule liegen. Dabei sollten sie genau auf die Richtung der Schatten achten, denn in manchen Schulen sehen die Schüler die Sonne mittags im Norden stehen und die Schatten sind nach Süden gerichtet – im Gegensatz zu den Schulen im deutschsprachigen Raum.
Mithilfe der Angaben für die eigene und die Partnerschule die Zeichnung des Eratosthenes erstellen
Jetzt geht es darum, die Zeichnung des Eratosthenes mit Hilfe der Angaben für ihren eigenen Ort und denjenigen des Ortes der gewählten Partnerschule zu erstellen. Die Kinder fertigen, für einen bestimmten Tag und nach dem gleichen Prinzip wie vorher, eine Zeichnung wie in Abb. 5 an.
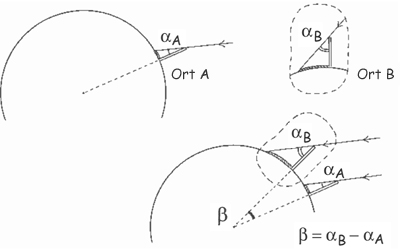
Abb. 5: Wie man den Abstand zwischen der eigenen Schule (Ort A) und der Partnerschule (Ort B) herausfindet
Lassen Sie die Kinder die auf Pauspapier gezeichneten Gnomone und Schatten auf den Erdkreis legen. Es ist wichtig, dass die Erde durch einen sehr großen Kreis (oder Halbkreis) dargestellt wird, denn die beiden Winkel werden sich nur durch einige Grade voneinander unterscheiden, wenn beide Schulen nicht allzu weit voneinander entfernt liegen.
Achtung! Für manche Schulen, die in der tropischen Zone oder auf der Südhalbkugel liegen, werden die Schüler den Schatten nach Süden gerichtet und die Sonne dementsprechend im Norden stehen sehen; in den Tropen ändert sich dies sogar zweimal im Jahr! Sie müssen also gut darauf achten, welche Schattenrichtung für die Partnerschule angegeben wurde, denn dadurch ändert sich die Rechnung: Sehen Sie sich noch einmal die Überlegungen zur Zeichnung des Eratosthenes an und platzieren Sie eine Stadt auf der Südhalbkugel auf den gleichen Meridian wie Alexandria. Da der Schatten dort in die umgekehrte Richtung zeigt, lassen Sie die Schüler den Winkel zwischen den Sonnenstrahlen und der Senkrechten in dieser Stadt einzeichnen (oder messen), ebenso den vom Mittelpunkt der Erde ausgehenden Winkel zwischen dieser Stadt und Alexandria. Auch bei dieser Aufgabe geht es darum, die Beziehung zwischen diesen Winkeln zu finden: Diesmal müssen die Winkelgrößen addiert werden, um den Winkel zwischen den beiden Städten im Erdmittelpunkt zu erhalten.
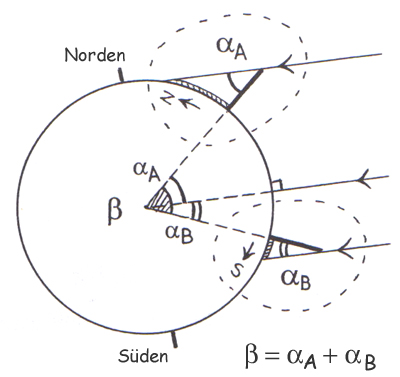
Abb. 6: Wenn die eine Schule nördlich und die andere südlich von Syene liegt, muss man etwas anders vorgehen!
Zur Überprüfung dieses Sachverhalts kann man den zwischen den beiden Städten einfallenden und durch den Erdmittelpunkt gehenden Sonnenstrahl einzeichnen: Er spielt die Rolle von Syene, da er der Senkrechten folgt. Er teilt den Winkel zwischen den beiden Städten im Erdmittelpunkt in zwei Teile: Wendet man das mit dem Städtepaar Alexandria-Syene entdeckte Prinzip der Winkelgleichheit auf die beiden Teilwinkel an, stellt man fest, dass der erste (obere) Winkel dem in der Stadt im Norden gemessenen Winkel entspricht, und der zweite dem in der Stadt im Süden gemessenen Winkel. Die beiden Teilwinkel zusammengenommen ergeben den ganzen Winkel.
Fassen wir zusammen: Zeigen die Schatten der Partnerschulen in die gleiche Richtung (beide nach Norden oder beide nach Süden), muss man die zwischen den Sonnenstrahlen und den Senkrechten gemessenen Winkel voneinander abziehen, um den Winkel im Erdmittelpunkt zu erhalten. Zeigen die Schatten in entgegengesetzte Richtungen, muss man die Winkel addieren.
Die Entfernung zwischen den Partnerstädten bestimmen
Wie bei Eratosthenes braucht man nur den Dreisatz anzuwenden (siehe vorherige Unterrichtseinheit), um anhand der Entfernung zwischen den beiden Städten (genauer: der Entfernung zwischen den Breitengraden dieser beiden Städte) die Länge des Erdumfangs zu finden. Sie müssen also diese Entfernung zwischen den beiden Städten kennen. Bei Eratosthenes lagen die zwei Städte (nahezu) auf dem gleichen Meridian (Längengrad). In Ihrem Fall aber ist es nicht sehr wahrscheinlich, dass Ihre Partnerschule auf dem gleichen Meridian liegt wie Ihre eigene. In solch einem Fall muss man die Entfernung zwischen den durch die beiden Partnerstädte gehenden Breitengraden (also den waagerecht eingezeichneten Parallelen auf einer Karte) und nicht die direkte Entfernung zwischen den Städten einsetzen.
(Um sich davon zu überzeugen, können die Kinder sich überlegen, welche auf ihrem Meridian liegende imaginäre Stadt den gleichen Winkel messen wird wie ihre Partnerschule. Es ist die Stadt, die auf dem gleichen Breitengrad liegt wie die Partnerstadt. In dieser Stadt erreicht die Sonne ihren Höchststand zur gleichen Zeit wie in ihrer eigenen, und sie können sie in ihre Zeichnung einzeichnen, da es sich ja bei der Zeichnung um einen durch einen Meridian (den durch ihre eigene Stadt) gehenden Schnitt der Erde handelt).
Ihre Schüler können einen Atlas oder eine Straßenkarte zu Hilfe nehmen, um die Entfernung zwischen dem Breitengrad ihrer Schule und demjenigen der Partnerschule herauszufinden (Achtung: Maßstab der jeweiligen Karte beachten!). Sie sollten mit Weltkarten vorsichtig sein, auf denen die Kontinente deformiert dargestellt sind und dadurch die Entfernungen nicht richtig wiedergeben werden.
Anmerkung:
Eine Breitengraddifferenz von
1° entspricht einer Entfernung von 111 Kilometer. Damit können Sie
abschätzen, ob die Entfernungsbestimmung Ihrer Schüler
einigermaßen stimmt.
Den Erdumfang berechnen
Es sind jetzt alle Zutaten vorhanden, um die Rechnung durchführen zu können. Es fehlt nur noch der Faktor, mit dem die Entfernung zwischen den Breitengraden multipliziert werden muss, um auf den Wert für den Erdumfang zu kommen. Dazu können die Kinder, wenn sie wollen, auf die im Abschnitt "Wie Eratosthenes den Umfang der Erde gemessen hat" erläuterten Methoden zurückgreifen, um wieder zu den Ergebnissen des Eratosthenes zu gelangen, oder einfach den Dreisatz anwenden (falls sie das Prinzip dieser Rechenmethode verstanden haben).
Den Durchmesser der Erde berechnen
Nichts einfacher als das. Die Kinder haben den Umfang unseres Planeten berechnet. Jetzt brauchen sie diesen nur noch durch die berühmte Zahl 'pi' (π = 3,141592654) zu teilen, und schon haben sie den Durchmesser der Erde.
Eratosthenes hatte seinerzeit genau 250 000 Stadien für den Erdumfang gefunden. Diese "schön runde" Zahl macht deutlich, dass ihm eine gute Größenordnung wichtiger war als Präzision. Und damit ist ihm ein Meisterstück gelungen, denn dies entspricht einer Länge von etwas mehr als 39 000 km und ergibt einen Erddurchmesser von ungefähr 12 500 km (siehe dazu auch die Anmerkung im Abschnitt "Wie Eratosthenes den Umfang der Erde gemessen hat").
Die Kinder können ihre eigenen Ergebnisse mit demjenigen von Eratosthenes vergleichen und mit den neuesten Messungen heutiger Wissenschaftler. (Dabei werden sie übrigens entdecken, dass die Erde nicht vollkommen rund ist wie eine Kugel, sondern an den Polen abgeplattet ist, sodass ihr polarer Durchmesser etwas geringer ist als ihr äquatorialer Duchmesser.) Sie können sich auch per E-Mail mit den Schülern der Partnerschule austauschen, um mit ihnen über ihre Ergebnisse und ihre schlauen Rechnungen zu diskutieren.
Sie können den Erdumfang immer wieder berechnen, wenn sie zeitgleich mit einer anderen Schule Messungen durchgeführt haben. Sind keine Messwerte vom gleichen Tag vorhanden, können sie (zwischen Mai und Juli) zur Not auch Messwerte vom Tag vor oder nach ihren Messungen verwenden. Der gemessene Winkel ändert sich während dieser Zeit sehr wenig von einem Tag zum anderen.
Weicht das Ergebnis für den Erdumfang stark von der Wirklichkeit ab, suchen Sie mit Ihren Schülern nach der/den möglichen Ursache/n der/des Fehler/s: ungenaue Winkelmessungen, ungenaue Messung der Entfernung zwischen den Partnerschulen usw. Veröffentlichen Sie Ihre Ergebnisse auf unserer Internetseite und diskutieren Sie darüber via Internet mit Ihren Partnern und mit uns.
Veröffentlichung der Messwerte
Auf den Internetseiten des Eratosthenes-Projektes können Ihre Schüler ihre Ergebnisse in eine "Tabelle aller Messwerte" eintragen, die speziell für die am Projekt beteiligten Schulen eingerichtet worden ist. Diese Tabelle enthält u.a. eine Spalte, in die Ihre Schüler ihren gemessenen und berechneten Wert für den Erdumfang veröffentlichen können (in km). Ihr Wert kann dann ab sofort auch von allen anderen Schulen gesehen und für Berechnungen verwendet werden.
Letzte Aktualisierung: 24.9.2024






