Wie Eratosthenes den Umfang der Erde gemessen hat

Publikation:	27.10.2007
Lernstufe:	3
Herkunft:	La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos

Die Senkrechte im Maßstab der Erde

Wenn die Kinder über den ihnen vorgelegten Text diskutieren, werden sich ihnen zahlreiche Fragen aufdrängen. Da ist zunächst der Begriff der Senk­rechten in den beiden Städten Syene und Alexandria. Wenn sie die Aktivitäten zu den Begriffen "senkrecht" und "waagerecht" aufmerksam verfolgt haben, dann haben sie bestimmt eine gute Vorstellung von der örtlichen Senkrechten. Aber wie sieht das im Maßstab unseres Planeten aus, wenn von der Senkrech­ten an verschiedenen Stellen unseres Planeten die Rede ist?

Stellen Sie den Kindern folgende Fragen: Wenn die Gnomone genau justiert sind (die Schüler sollen sich nötigenfalls noch einmal die betreffende Aktivität und die entsprechenden Notizen in ihren Versuchsheften ansehen), wie stehen sie dann in Bezug auf ihre waagerechte Unterlage? Die Kinder werden ohne zu zögern antworten, dass die Gnomone senkrecht stehen und damit auch senk­recht (im rechten Winkel) zum waagerechten Boden. "Wie ist es dann bei Gno­monen, die sich an verschiedenen Orten auf der Erde befinden?"

Die Schüler sollen über diesen Punkt diskutieren und ihre Vermutungen in ihre Versuchshefte notieren. Diese Vermutungen versuchen sie anschließend expe­rimentell zu bestätigen. Hierzu können sie von einem einfachen Pappstreifen ausgehen, den sie flach auf den Boden legen und auf den sie senkrecht kleine Stäbchen oder Reißzwecken kleben. Diese stellen die justierten Gnomone dar. Da sie ja wissen, dass die Erde nicht flach ist, krümmen sie den Streifen und sehen, dass die Gnomone nicht mehr parallel zueinander stehen, sondern in verschiedene Richtungen zeigen. Sie schließen den Streifen zu einem Reifen und sehen dann gewissermaßen um die Erde verteilte Gnomone. Sie zeichnen dann in ihr Versuchsheft dieses eigenartige Bild der Erde, die jetzt wie ein Igel mit Stacheln aussieht.

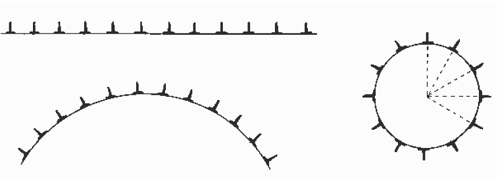
Abb. 1: Ein Streifen mit vielen kleinen Gnomonen und wie daraus eine "Igel-Erde" mit "Gnomonen-Stacheln" wird

Nachdem die Kinder erkannt haben, dass all diese Gnomone an jedem Punkt der Erde die Richtung der Senkrechten anzeigen, fragen Sie sie, was ge­schieht, wenn sie die Stacheln im Geist bis ins Erdinnere verlängern. "Sie treffen sich alle im Mittelpunkt der Erde!" Dies lässt sich nachprüfen, wenn man das vorige Experiment wiederholt und die Stäbchen oder Reißzwecken z. B. durch Stricknadeln oder Spieße ersetzt.

Die Schüler schließen daraus, dass die Senkrechte an jedem Ort unserer Erde zum Mittelpunkt unserer Erde zeigt und dass die Gnomone in zwei verschiede­nen Städten nicht parallel zueinander stehen, sondern einen Winkel bilden.

Zeichnen Sie dann den "Erd-Kreis" an die Tafel und fragen Sie, wo – nach dem, was sie über die Messungen des Eratosthenes wissen – auf diesem Kreis die Städte Syene und Alexandria einzuzeichnen sind.

Das Geheimnis des Eratosthenes entdecken

Die folgende Aufgabe ist schwierig. Sie sollten den Kindern helfen, den Weg zur berühmten Zeichnung des Eratosthenes zu finden.

In den kleinen historischen Texten hieß es, dass in Syene am 21. Juni zum Sonnenmittag die Sonnenstrahlen auf den Boden eines Brunnenschachts fielen und senkrecht stehende Gegenstände keine Schatten warfen. Die Sonnen­strahlen kamen also genau senkrecht von oben. Die Kinder zeichnen auf ein DIN A4- oder DIN A3-Blatt den Erd-Kreis wie auf der ersten Skizze der Abb. 2. Dann zeichnen sie mehrere (zueinander genau parallele) Sonnenstrahlen ein, von denen einer genau der Senkrechten in Syene entspricht.

(Man kann auch zuerst auf ein großes Blatt Papier die parallelen Sonnenstrah­len zeichnen. Dann schneidet man aus farbiger Pappe eine "Erdscheibe" aus und befestigt sie auf dem Blatt, indem man eine Nadel durch ihren Mittelpunkt sticht. Danach dreht man die Erde so, dass die Sonnenstrahlen senkrecht auf Syene treffen.)

Wo zeichnet man jetzt Alexandria ein? Fragen Sie die Kinder, was Eratosthenes an diesem selben Tag zur gleichen Zeit gemessen hat. "Den Winkel zwischen den Sonnenstrahlen und dem Obelisken, also den Winkel, den diese Strahlen mit der Senkrechten bilden." Jetzt braucht man sich nur die Größe dieses Win­kels in Erinnerung zu rufen (7,2°) und eine Zeichnung des Winkels anzuferti­gen, wie in Abb. 2 oben rechts. Die Kinder zeichnen den Winkel von Alexandria auf Pauspapier und legen ihn dann so auf ihre Zeichnung mit den Sonnenstrah­len, dass der auf den Obelisken fallende Sonnenstrahl parallel zu demjenigen in Syene ist.

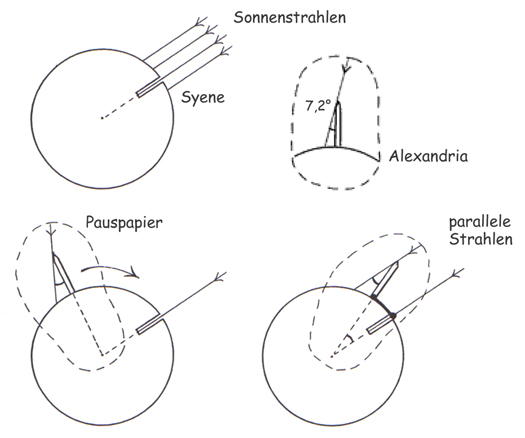
Abb. 2: Wie kann man herausfinden, wo Alexandria liegt, wenn man weiss, wo Syene ist und welchen Winkel der Schatten des Obelisken hat?

Das Geheimnis des Eratosthenes: Nachdem sie die Lage Alexandrias gekenn­zeichnet haben, ziehen sie die durch diese Stadt gehende Senkrechte (die Verbindungslinie von Alexandria zum Erdmittelpunkt). Fragen Sie Ihre Schüler jetzt, was sie von dem Winkel zwischen dieser Senkrechten und der Senkrech­ten, die durch Syene geht, halten. "Er gleicht ziemlich genau dem auf Paus­papier gezeichneten, also dem von Eratosthenes gemessenen Winkel."

Das wollen sie sofort überprüfen: Sie drehen das Pauspapier um und legen den Winkel über den am Erdmittelpunkt eingezeichneten Winkel. Und siehe da, die beiden Winkel sind deckungsgleich. Dies ist also das Geheimnis des Eratosthe­nes! Lassen Sie die Kinder nachprüfen, dass sie mit einer anderen Winkelgröße (der doppelten zum Beispiel) das gleiche Ergebnis erzielen. Sie positionieren das "neue Alexandria" so, dass sich ein Winkel von 14° ergibt, ziehen die Senk­rechte und messen den neuen Winkel am Erdmittelpunkt. Hierfür können sie auch einen Winkelmesser benutzen.

Stolz darüber, das Geheimnis von Eratosthenes wiederentdeckt zu haben, übertragen sie die Zeichnung ohne unnötige Hilfslinien in ihr Versuchsheft. Auch die Schlussfolgerung, die das Geheimnis des Eratosthenes darstellt, wird hinzugefügt: Der in Alexandria gemessene Winkel zwischen den Sonnenstrahlen und der Senkrechten ist genauso groß wie der im Erdmittelpunkt gemessene Winkel zwischen Alexandria und Syene. Sie sehen auf ihrer Zeichnung das "Z wie Zorro", das ihnen bestimmt helfen wird, sich dieses unglaubliche Fazit einzuprägen.

Zusatzfrage: Wie würde es sich auf diese beiden Winkel auswirken, wenn man die Erde sich so drehen ließe, dass die Sonnenstrahlen nicht mehr senkrecht auf Syene treffen (d. h. wenn man den Erd-Kreis im entgegengesetzten Uhr­zeigersinn drehte)?

Die Kinder wiederholen das Experiment. Sie zeichnen die neuen Winkel, verglei­chen sie und stellen fest, dass sie nicht mehr gleich sind, denn in Syene er­scheint ein zusätzlicher Winkel und verändert die Voraussetzungen.

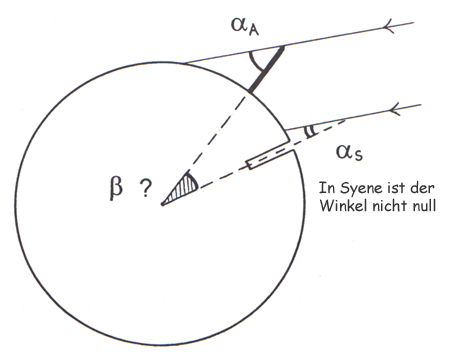
Abb. 3: Wenn die Strahlen nicht mehr senkrecht in Syene einfallen, muss sich auch in Alexandria etwas ändern.

Wenn die Schüler die neuen Winkel in Syene und Alexandria auf Pauspapier zeichnen und dann versuchen, diese über den Winkel β im Erdmittelpunkt zu legen und durch Probieren eine Kombination zu finden, bei denen sie zusam­menpassen, erkennen sie vielleicht ganz ohne Hilfestellung Folgendes: Dass der im Erdmittelpunkt gemessene Winkel β zwischen beiden Städten gleich der Differenz zwischen den in beiden Städten gemessenen Winkeln α_A und α_S zwi­schen den Strahlen und den Gnomonen ist (sofern die Schatten der Gnomone in beiden Städten in die gleiche Richtung zeigen, also z. B. beide nach "Nor­den", anderenfalls ist der Winkel im Erdmittelpunkt gerade die Summe der beiden Schattenwinkel). Man kann dies dann auch noch einmal mit dem Win­kelmesser rechnerisch überprüfen.

Sie haben auf diese Weise die Schlussfolgerung des Erastothenes sogar auf die (am häufigsten auftretenden) Fälle ausgedehnt, in denen die Sonnenstrahlen in keinem der beiden Orte, in denen Messungen durchgeführt werden, senk­recht einfallen! Sie notieren auch diese Entdeckung in ihre Versuchshefte; sie wird ihnen sehr nützlich sein, wenn sie die Skizze des Eratosthenes für ihre eigenen Messwerte und diejenigen einer Partnerschule zeichnen müssen.

Damit sind Ihre Schüler jetzt gewappnet, um in allen vorkommenden Fällen den Umfang der Erde zu messen.

Die Länge des durch Syene und Alexandria gehenden Meridians bestimmen

Zur Vorbereitung auf die Dreisatzrechnung, die für die Berechnung des Meri­dians (also für die Messung des Erdumfangs) unverzichtbar ist, lassen Sie Ihre Schüler über folgendes Szenario nachdenken:

"Stellt euch vor, Eratosthenes hätte in Alexandria einen anderen Winkel ge­messen, und stellt euch weiter vor, Syene und Alexandria lägen auf einer Erde, die einer in 8 gleiche Teile aufgeschnittenen Torte gleicht, und zwar an den in Abb. 4 dargestellten Stellen. Wie findet man die Länge des Gesamt­umfangs dieser Torte heraus, wenn man weiß, wie lang der Rand eines Tor­tenstücks ist?"

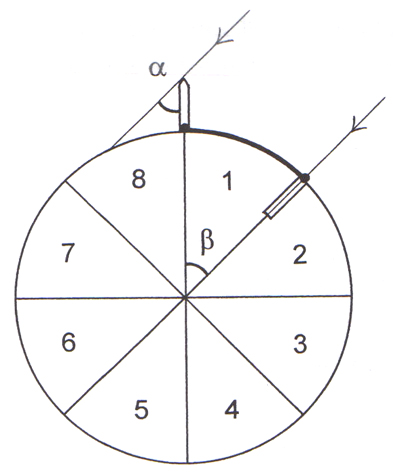
Abb. 4: Wie groß ist der Erdumfang, wenn der Abstand der beiden Orte gerade ein Tortenstück groß ist?

"Das ist einfach, man braucht die Länge des Randes des Tortenstücks nur mit 8 zu multiplizieren", wird man Ihnen antworten. "Seid ihr euch dessen so si­cher?" Um dies nachzuprüfen, können Sie vorschlagen, einen großen Kreis in acht gleiche Abschnitte zu teilen und dann mit einer Schnur die Länge des Randes eines Abschnitts und mit einer anderen Schnur die Länge des Gesamt­umfangs zu messen. Sie werden ein Verhältnis von 8:1 zwischen den Längen der beiden Schnüre herausbekommen.

Genau dies hat auch Eratosthenes erkannt. Aber wie viele Tortenstücke gibt es in Wirklichkeit?

Die Schüler können mehrere Experimente vorschlagen, um dies herauszufinden, und sie können Gruppen bilden, um die diversen Vorschläge auszuprobieren.

• Man kann die Tortenstücke nach dem Winkelmaß von 7,2° bemessen und zählen, in wie viele Stücke man die Erde dann schneiden müsste.
• Man kann mit einer Schnur (siehe Abb. 4) die Länge des Randes des Stücks Syene–Alexandria messen und mit der Länge des Gesamtumfangs der Erde vergleichen.
• Diejenigen, die lieber rechnen, werden 360° (den gesamten Kreisumfang) durch 7,2° (den im Erdmittelpunkt gemessenen Winkel) dividieren.

Sie werden genau einen Faktor 50 herausbekommen (zumindest rechnerisch).

Jetzt braucht man nur noch den Dreisatz anzuwenden. Eratosthenes sagt uns, dass die Entfernung zwischen Syene und Alexandria 5 000 ägyptische Stadien beträgt. Multipliziert man diese Entfernung mit 50, erhält man genau 250 000 Stadien, wie bereits der große griechische Gelehrte herausgefunden hatte. Damit ist endlich das Rätsel gelöst.

Aber wie lang war eigentlich das ägyptische Stadion? Diese letzte Nachfor­schung wird sie zu Enzyklopädien und Suchmaschinen im Internet greifen las­sen, und sie werden folgenden Wert finden: 1 ägyptisches Stadion = 157,5 m, womit sich ein Erdumfang von 39 375 km ergibt. Vergleichen Sie diesen Wert schnell mit den in Lexika oder im Internet angegebenen Zahlen für den Erdum­fang und Sie werden sich der unglaublichen Präzision dieser Messung bewusst werden.

Anmerkung:
Es ist leider nicht zweifelsfrei überliefert, welchen Wert für den Erdumfang Eratosthenes genau herausbekommen hat. Es gab nämlich damals eine ganze Menge verschiedener als "Stadion" bezeichnete Längen (genauso, wie es heute auch noch verschieden lange "Meilen" gibt). In der griechischen Welt benutzte man üblicherweise das attische Stadion, das einer Länge von ca. 178 Metern entsprach. Es gab aber auch zum Beispiel das phönizisch-ägyptische Stadion (209 m), das babylonisch-persische Stadion (196 m), das olympische Stadion (192 m), das römische Stadion (185 m) oder das mesopo­tamische Stadion (149 m). Anderen Quellen zufolge maß das ägyptische Sta­dion 157,5 Meter. Mit letzterem Wert für die Länge eines Stadions stimmt der von Eratosthenes berechnete Erdumfang am besten mit dem heute bekannten Wert überein. Allerdings ist es recht wahrscheinlich, dass er als griechischer Gelehrter das attische Stadion verwendete, was immer noch zu einem – für die damals mögliche "Messgenauigkeit" – erstaunlich genauen Wert für den Erdum­fang führt.

© Sonnentaler/La main à la pâte | Impressum | Disclaimer | Datenschutz | RSS | E-Mail

© Sonnentaler / La main à la pâte  http://www.sonnentaler.net/