Entwicklung der Temperatur auf der Erde
| Autoren: | |
| Publikation: | 3.12.2013 |
| Herkunft: | Sonnentaler |
Letzte Aktualisierung: Diese Seite wurde am 26.1.2026 entsprechend der neuesten zur Verfügung stehenden Daten aktualisiert.
Die langjährigen Temperaturmessreihen der meteorologischen Dienste auf der ganzen Welt zeigen: Die Erde wird immer wärmer. Aber wie berechnet man, um wie viel Grad die globale Temperatur [1] bzw. die Temperatur an einem bestimmten Ort über einen bestimmten Zeitraum gestiegen ist? Und wie genau ist diese Aussage? Das wollen wir im Folgenden erläutern.
Vorab: Definition des Begriffs "Klima"
Temperaturen können von Jahr zu Jahr stark schwanken. Um zu verfolgen, wie und ob sich das Klima verändert, beobachtet man die Temperaturentwicklung über einen längeren Zeitraum. Die folgende Definition fasst die Klimadefinition der Weltorganisation für Meteorologie (WMO) zusammen [2]:
Das Klima ist das "durchschnittliche Wetter". Das Klima an einem bestimmten Ort wird beschrieben durch die über einen längeren Zeitraum erfassten statistischen Mittelwerte und Schwankungen relevanter Größen wie Temperatur, Niederschlag und Wind. Der betrachtete Zeitraum beträgt mindestens 30 Jahre.
Die Entwicklung der mittleren Temperatur auf der Erde
Das Goddard-Institut für Weltraumstudien der NASA sammelt die Temperaturdaten zahlreicher Wetterstationen weltweit und berechnet daraus die mittlere Temperaturänderung auf der Erde: zum einen die mittlere Temperaturänderung an der Landoberfläche und zum anderen die mittlere Temperaturänderung an der Land- und der Ozeanoberfläche (siehe Abb. 6).
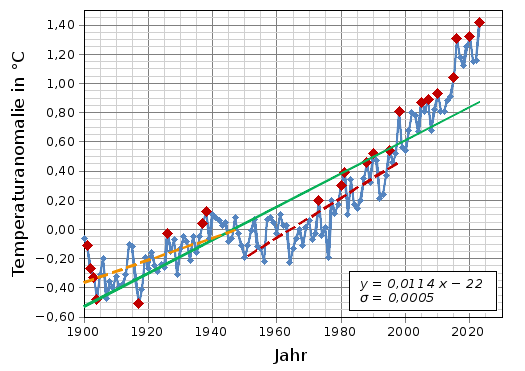
Abb. 1: Mittlere Jahrestemperaturanomalie auf der Landoberfläche der Erde zwischen 1900 und 2025 (bezogen auf den Mittelwert der Jahre 1951-1980, → Tabelle); grüne Linie: linearer Trend 1900 bis 2025, orange gestrichelte Linie: linearer Trend 1900 bis 1950, rote gestrichelte Linie: linearer Trend 1951 bis 2000 (zum Vergrößern auf das Diagramm klicken); die mit roten Rhomben markierten Datenpunkte zeigen an, dass es in dem entsprechenden Jahr kälter bzw. wärmer war als in allen Jahren davor; Datenquelle: Goddard Institute for Space Studies.
In Abb. 1 ist durch die Messpunkte eine Ausgleichsgerade gelegt worden – eine sogenannte Regressionsgerade bzw. ein linearer Trend [4]. Die Regressionsgerade ist charakterisiert durch ihre Gleichung (y = m x + b) und die Standardabweichung (σ) [5]. Vereinfacht ausgedrückt: Man versucht durch die Messpunkte eine Gerade zu legen, die möglichst nah an allen Punkten ist. Wie gut die gefundene Gerade "passt", wird durch die Standardabweichung angegeben.
Für die Regressionsgerade (grüne Linie) in Abb. 1 ist:
y = 0,012175 x − 23,70 und
σ = 0,000545
Dabei steht y für die Temperaturanomalie in °C und x für das Jahr. Aus der Steigung der Geraden kann man ablesen, dass zwischen 1900 und 2025 die Temperatur im Mittel um 0,012175 °C pro Jahr gestiegen ist.
Mit Hilfe der Standardabweichung [5] kann man angeben, wie sicher es ist, dass der Temperaturanstieg tatsächlich m = 0,0122 °C pro Jahr beträgt:
- Mit einer Wahrscheinlichkeit von 68,3% liegt der wahre Wert zwischen m − σ und m + σ, also zwischen 0,0116 °C und 0,0127 °C pro Jahr.
- Mit einer Wahrscheinlichkeit von 95,4% liegt er zwischen m − 2σ und m + 2σ, also zwischen 0,0111 °C und 0,0133 °C pro Jahr.
- Und mit einer Wahrscheinlichkeit von 99,7% liegt er zwischen m − 3σ und m + 3σ, also zwischen 0,0105 °C und 0,0138 °C pro Jahr [6].
Wir geben im Folgenden den Temperaturanstieg mit einem Fehler an, der der doppelten Standardabweichung entspricht (95,4% Sicherheit). Der Anstieg der mittleren Temperaturanomalie auf der Erde zwischen 1900 und 2025 beträgt demnach: (0,0122 ± 0,0011) °C pro Jahr.
Da dieser Wert sehr klein ist, kann man stattdessen auch den Temperaturanstieg in 100 Jahren angeben, der entsprechend 100 Mal größer ist. Die Aussage lautet dann: Im Zeitraum zwischen 1900 und 2025 ist die Temperatur auf der Erde um (1,22 ± 0,11) °C pro 100 Jahre gestiegen.
In der folgenden Tabelle sind die Werte für die Temperaturerhöhung für verschiedene Zeiträume bzw. unterschiedliche Orte angegeben. Es steht hier explizit Temperaturerhöhung und nicht Temperaturveränderung, weil in allen Fällen die Temperatur eindeutig gestiegen ist.
| Ort und Zeitraum |
Temperaturerhöhung pro
Jahr ± doppelte Standardabweichung [5] |
Temperaturerhöhung pro
100 Jahre ± doppelte Standardabweichung [5] |
Temperaturerhöhung im angegebenen Zeitraum |
|---|---|---|---|
| Erde 1900–2025 | 0,0122 °C ± 0,0011 °C | 1,22 °C ± 0,11 °C | 1,52 °C ± 0,14 °C |
| Erde 1900–1950 | 0,0078 °C ± 0,0023 °C | 0,78 °C ± 0,23 °C | 0,39 °C ± 0,12 °C |
| Erde 1951–2000 | 0,014 °C ± 0,003 °C | 1,4 °C ± 0,3 °C | 0,69 °C ± 0,13 °C |
| Erde 1900–2000 | 0,0078 °C ± 0,0010 °C | 0,78 °C ± 0,10 °C | 0,78 °C ± 0,10 °C |
| Basel 1900–2025 | 0,022 °C ± 0,003 °C | 2,2 °C ± 0,3 °C | 2,7 °C ± 0,4 °C |
| Berlin 1900–2025 | 0,015 °C ± 0,004 °C | 1,5 °C ± 0,4 °C | 1,8 °C ± 0,5 °C |
| Wien 1900–2025 | 0,022 °C ± 0,004 °C | 2,2 °C ± 0,4 °C | 2,8 °C ± 0,4 °C |
Tab. 1: Temperaturerhöhung auf der Erde sowie in Basel, Berlin und Wien für verschiedene Zeiträume. Die Quellen für die Temperaturdaten sind bei den Abbildungen auf dieser Seite angegeben.
Temperaturentwicklung seit 1900 in Basel, Berlin und Wien
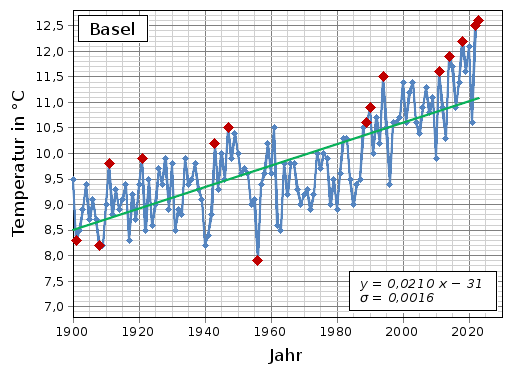
Abb. 2: Mittlere Jahrestemperatur in Basel (Messstation Binningen) zwischen 1900 und 2025 (→ Tabelle), zum Vergrößern auf das Diagramm klicken; die mit roten Rhomben markierten Datenpunkte zeigen an, dass es in dem entsprechenden Jahr kälter bzw. wärmer war als in allen Jahren davor; Datenquelle: MeteoSchweiz.
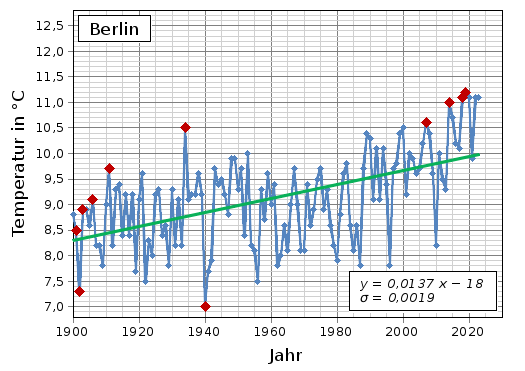
Abb. 3: Mittlere Jahrestemperatur in Berlin (Messstation Dahlem) zwischen 1900 und 2025 (→ Tabelle), zum Vergrößern auf das Diagramm klicken; die mit roten Rhomben markierten Datenpunkte zeigen an, dass es in dem entsprechenden Jahr kälter bzw. wärmer war als in allen Jahren davor; Datenquelle: Institut für Meteorologie der Freien Universität Berlin
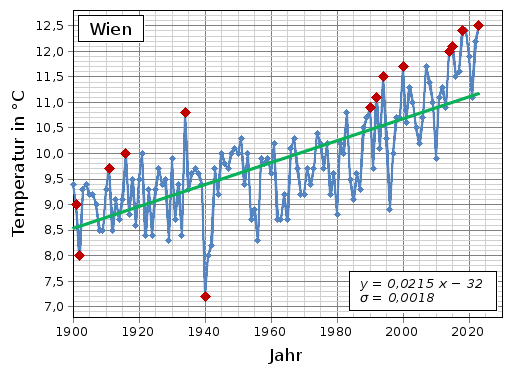
Abb. 4: Mittlere Jahrestemperatur in Wien (Messstation Hohe Warte) zwischen 1900 und 2025 (→ Tabelle), zum Vergrößern auf das Diagramm klicken; die mit roten Rhomben markierten Datenpunkte zeigen an, dass es in dem entsprechenden Jahr kälter bzw. wärmer war als in allen Jahren davor; Datenquelle: ZAMG/HISTALP.
Temperaturentwicklung und gleitender Mittelwert
Eine weitere Methode, die Temperaturentwicklung auf der Erde zu analysieren, besteht darin, den 30-jährigen gleitenden Temperaturmittelwert zu bilden (siehe die rote Linie in Abb. 5). Diese Methode wird der Definition des Klimabegriffs gerecht. Für 1895 zum Beispiel wurden die Werte für die Jahre 1880 bis 1909 gemittelt, für 1896 die Werte für die Jahre 1881 bis 1910 und so weiter und so fort (immer 15 Jahre vor dem betrachteten Jahr, das Jahr selbst und 14 Jahre nach dem betrachteten Jahr). Auch hier ist deutlich ein stetiger Anstieg der Temperatur zu erkennen.
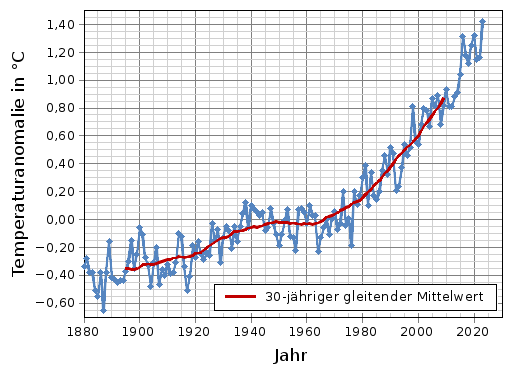
Abb. 5: Mittlere Jahrestemperaturanomalie auf der Erde zwischen 1880 und 2025 (blau) , bezogen auf den Mittelwert der Jahre 1951-1980, sowie 30-jähriger gleitender Mittelwert (rote Kurve), weitere Erklärung im Text, zum Vergrößern auf das Diagramm klicken); Datenquelle: Goddard Institute for Space Studies.
Im Gegensatz zu allen anderen Abbildungen auf dieser Seite, in denen immer die Temperatur bzw. die Temperaturanomalie an der Landoberfläche (engl.: Land-Surface Air Temperature Anomaly) aufgetragen ist, zeigt Abb. 6 die Entwicklung des sogenannten "Land-Ocean Temperature Index" (LOTI). Beim LOTI werden für den Temperaturmittelwert die Temperaturmesswerte für die Landoberfläche und die Ozeanoberfläche kombiniert.
Da die Ozeane etwa zwei Drittel der Erdoberfläche bedecken, gibt eine kombinierte Temperatur aus Erd- und Ozeanoberflächentemperatur ein realistischeres Bild der Erwärmung unseres Planeten wieder. Wegen der hohen Wärmekapazität von Wasser, erwärmt sich unser Planet etwas weniger schnell (blaue Kurve in Abb. 6), als durch die an Land gemessene Temperaturerhöhung angedeutet wird (braune Kurve in Abb. 6).
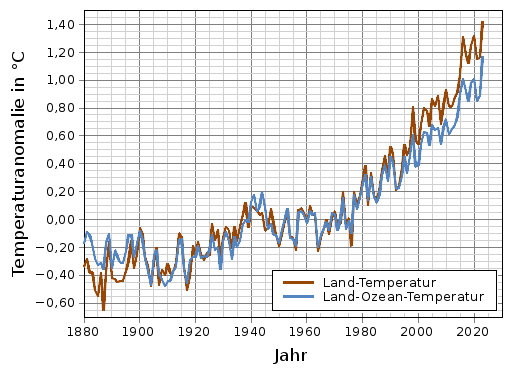
Abb. 6: Mittlere Land/Ozean-Jahrestemperaturanomalie (blaue Kurve) und mittlere Land-Jahrestemperaturanomalie (braune Kurve) zwischen 1880 und 2025, (jeweils bezogen auf den Mittelwert der Jahre 1951-1980); zum Vergrößern auf das Diagramm klicken; Datenquelle: Goddard Institute for Space Studies.
Weitere Informationen
- KlimaLounge: Experten auf dem Gebiet der Klimatologie berichten in diesem Wissenschaftsblog allgemeinverständlich über die aktuellen Ergebnisse und Erkenntnisse rund um den Klimawandel.
- Informationsportal Klimawandel der ZAMG (österreichischen Zentralanstalt für Meteorologie und Geodynamik) und dort insbesondere die FAQ
- MeteoSchweiz: Klimawandel
- Deutscher Klimaatlas des Deutschen Wetterdienstes
Fußnoten
1: Die globale Temperatur ist die über viele – gleichmäßig über die Erde verteilte – Orte gemittelte Temperatur.
2: World Meteorological Organization (WMO)
3: In der Tabelle des Goddard Institute for Space Studies kann man die Werte für jeden Monat seit Januar 1880 ablesen – oder direkt die jährlichen Mittelwerte. Diese Daten werden ständig aktualisiert. In unserem Arbeitsblatt 4a sind die jährlichen Temperaturanomalien von 1900 bis heute übersichtlich dargestellt. Sie werden mehrmals pro Jahr an die NASA-GISS-Daten angeglichen.
Wenn man mit der Temperaturanomalie anstatt mit absoluten Temperaturen arbeitet, umgeht man die Problematik, bestimmen zu müssen, welches die mittlere Temperatur auf der Erde ist (welche Orte sollen für die Mittelwertbildung hinzugezogen werden?). Mit der Temperaturanomalie betrachtet man nur Differenzen und verschiebt lediglich den Nullpunkt der y-Achse.
4: Eine Regressionsgerade wird mathematisch durch eine
Funktionsgleichung der Form y = m x + b
beschrieben. Dabei ist m die Steigung der Geraden und b der
Schnittpunkt mit der y-Achse. In Abb. 1
entspricht y der Temperatur und x dem Jahr. Die
Steigung m entspricht somit der Temperaturänderung pro Jahr.
Es
gibt zahlreiche Möglichkeiten, sich eine Regressionsgerade ausgeben zu lassen:
mit Hilfe kleiner Programme auf dem Computer (QtiPlot zum Beispiel), mit Hilfe
von Tabellenkalkulationsprogrammen oder auch mit Hilfe von grafikfähigen
Taschenrechnern.
5: Wird für einen Wert m die Standardabweichung σ angegeben, so liegt der wahre Wert mit einer Wahrscheinlichkeit von 68,3% zwischen m − σ und m + σ. Mit einer Wahrscheinlichkeit von 95,4% liegt er zwischen m − 2σ und m + 2σ, und mit einer Wahrscheinlichkeit von 99,7% zwischen m − 3σ und m + 3σ.
6: Gibt man den Wert mit einer höheren Wahrscheinlichkeit an (99,7% anstatt 95,4%) ändert sich lediglich der Bereich der Messunsicherheit (die Fehlerangabe). Man kann also sagen, dass der wahre Temperaturanstieg mit einer Wahrscheinlichkeit von 95,4% zwischen 0,0111 °C und 0,0133 °C pro Jahr liegt, und mit einer Wahrscheinlichkeit von 99,7% zwischen 0,0105 °C und 0,0138 °C pro Jahr.
Letzte Aktualisierung: 2.2.2026






