Simulation des Sonnenmittags mit Hilfe eines Balls

Publikation:	3.4.2008
Lernstufe:	3
Dauer:	Zwei Unterrichtsstunden von je 30 Minuten (ohne die Eintragungen ins Ver­suchsheft) in einem etwas abgedunkelten Raum
Material:	Für jede Gruppe von 3-5 Schülern: 1. Unterrichtsstunde: ein größerer, glatter, einfarbiger Ball ein Zylinder aus starkem Tonkarton (der weiter als hoch ist), auf den der Ball gelegt wird Material für 5 oder 6 gleichartige "Minignomone" nicht höher als 1 cm (Polster- oder Flachkopfnägel, kleine Schrauben, Nieten, Streichholzstücke) Klebstoff (Patafix oder ähnliches), Knete eine Taschenlampe 2. Unterrichtsstunde: Das gleiche Material, außerdem eine "Minikarte" von Ägypten (durch Foto­kopie verkleinert) – die Entfernung Alexandria-Syene sollte ungefähr 1/7 des Ballumfangs betragen (mit einer Schnur nachmessen) – das ist mit Absicht mehr als auf einem Globus. Die "Minikarte" wird in der Mitte durch­geschnitten, so dass nur das Nildelta und das Niltal bis Syene übrigbleiben.
Herkunft:	La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos

Wenn Ihre Schüler von der vorhergehenden Simulation begeistert waren, so werden sie es von den folgenden noch mehr sein, geht es doch jetzt darum, mit einem Blick aus dem "Weltraum" die Auswirkungen der Drehung eines "Erd-Balls" um sich selbst zu beobachten. Dieser Erdball, auf dem die "Mini-Gno­mone" angebracht sind, wird von einer – dieses Mal statischen – "Sonnen-Lampe" angestrahlt. Im Vergleich zu den vorhergehenden Simulationen, bei denen die "Sonnen-Lampe" über der unbeweglichen platten "Erdoberfläche" bewegt wurde, sind bei der jetzigen Simulation die Bedingungen genau umge­kehrt.

1. Unterrichtsstunde

a) Mit dem Ball und der Lampe nachstellen, was beim Gnomon in der Sonne beobachtet wurde

Jede Gruppe befestigt an einer beliebigen Stelle des Balls einen Mini-Gnomon (z. B. eine Schraube), setzt den Ball auf den Zylinder aus Karton und stellt das Ganze auf einen Tisch. Damit der Zylinder sich auf dem Tisch nicht verschie­ben kann, wird er an vier Stellen mit Knete eingekeilt. Stellen Sie den Schülern folgende Aufgabe: "Der Ball wird von einer unbeweglichen Lampe angestrahlt. Findet heraus, wie ihr durch Drehen des Balls erreichen könnt, dass sich die Richtungen und Längen des Schatttens des Mini-Gnomons so verhalten, wie ihr es vorher mit eurem Gnomon in der Sonne beobachtet habt".

Dabei tauchen eine ganz Reihe sehr interessanter Fragen und Probleme auf: Wo muss der Ball in Bezug zur Lampe liegen? In welche Richtung muss er ge­dreht werden? Wie findet man den Zeitpunkt des Sonnenmittags heraus? Was tun, wenn dann der Schatten im Verhältnis zur Höhe der Schraube zu lang oder zu kurz ist? Seien Sie auf rege Diskussionen und vielfaches Ausprobieren gefasst. Aber die Kinder werden letztendlich alle Probleme lösen und mit Be­geisterung feststellen, dass sich der Schatten ihrer kleinen Schraube genau so verhält wie der Schatten ihres Gnomons in der echten Sonne. Bevor ihnen diese Simulation gelingt, müssen sie jedoch viele Dinge begriffen haben, vor allem, dass der Ball sich anders herum dreht als der Schatten, d. h. man muss ihn gegen den Uhrzeigersinn drehen, damit sich der Schatten – wie in der ech­ten Sonne – im Uhrzeigersinn dreht.

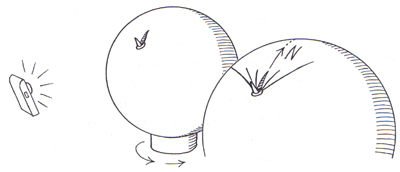
Abb. 6: Beim Drehen des Balls mit dem Mini-Gnomon kann man den Schattenver­lauf eines echten, in der Sonne aufgestellten Gnomons simulieren.

Einige Gruppen haben sicher schon mit einem Stift den Fächer der Minischat­tenumrisse der Schraube auf dem Ball eingezeichnet und sind vielleicht bereits auf die hervorragende Idee gekommen, mit einem bis zum "Nordpol" reichenden Pfeil die Nordrichtung zu markieren (wir werden später noch darauf zurückkom­men). Alle Kinder haben natürlich die "Tag-" und die "Nachtseite" des Balls be­obachtet und wie die Schraube "morgens" von der Nacht- zur Tagseite und "abends" von der Tag- zur Nachtseite wanderte.

b) Mehrere Mini-Gnomone so platzieren, dass sie gleichzeitig Sonnen­mittag haben

An dieser Stelle werden Ihre Schüler auf experimentellem Wege den Begriff Meridian bzw. Längenkreis erkunden (der Meridian entspricht einem halben Längenkreis). Der Ball mit der darauf befestigten Schraube und die Lampe stehen so, dass Sonnenmittag ist. Stellen Sie den Kindern jetzt folgende Aufgabe: "Nehmt eine zweite Schraube und findet heraus, an welcher Stelle auf dem Ball ihr sie befestigen müsst, damit sie überhaupt keinen Schatten wirft. Ball und Lampe dürfen dabei nicht bewegt werden. Befestigt anschlie­ßend noch 2 oder 3 weitere Schrauben auf dem Ball, für die ebenfalls Sonnen­mittag ist. Überprüft schließlich das Ganze, indem ihr den Ball dreht".

Die Schüler begreifen, dass die zweite Schraube die Rolle des Brunnens in Syene spielt, wohingegen die erste den Obelisken in Alexandria darstellt. Daher finden sie auch rasch heraus, dass die zweite Schraube "südlich" von der ers­ten Schraube befestigt werden muss. Diejenigen, die vorhin auf die Idee ge­kommen sind, eine Linie bis zum "Nordpol" zu ziehen, sehen sofort, dass die zweite Schraube irgendwo auf die Verlängerung dieser Linie gesetzt werden muss. Daher finden sie auch ohne größere Schwierigkeiten die Positionen für die weiteren Schrauben, die ebenfalls auf dieser Linie angebracht werden müssen.

Ganz nebenbei fallen ihnen interessante Dinge auf, die für den weiteren Verlauf des Projektes von Bedeutung sind: Dass die Schatten auf der zum "Nordpol" zeigenden Linie liegen, dass sie zu den "Polen" hin allmählich länger werden, und dass die Schatten der Schrauben, die "südlich" der zweiten (der Syene-Schraube) befestigt sind, zum "Südpol" zeigen.

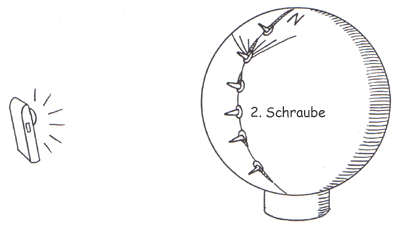
Abb. 7: An verschiedenen "Breitengraden" erhält man unterschiedliche Schatten­längen.

Fragen Sie die Kinder nun, was aus der Linie wird, die alle Schrauben miteinan­der verbindet, wenn man sie an beiden Seiten verlängert: "Sie wird den Ball umrunden!". Die Schüler sagen anschließend Folgendes voraus: Wenn man auf der Rückseite des Balls Schrauben auf dieser Linie befestigt und den Ball an­schließend dreht, werden auch diese Schrauben alle gleichzeitig den Sonnen­mittag erreichen. Diesen Sachverhalt werden die Kinder natürlich überprüfen.

Einige Schüler werden sich vielleicht die Frage stellen, was eigentlich mit einer "geneigten Erde" passiert, so wie sie sie vom Globus oder von Abbildungen in Sachbüchern her kennen? Sie können sich nur schwer vorstellen, dass auch dann die Schatten am Sonnenmittag zu den Polen zeigen, so wie es mit dem schön "geraden" Ball auf seinem Zylinder der Fall ist. Aber wie kann man das herausfinden? Am einfachsten – und am lustigsten – geht es, wenn man den Ball an den beiden "Polen" zwischen den Zeigefingerspitzen hält, ihn etwas neigt und mit Hilfe der Daumen dreht. Die Kinder stellen fest, dass, ganz gleich wie stark man den Ball neigt – man kann ihn sogar waagerecht halten –, die Schatten am "Sonnenmittag" immer auf den Meridian (Längenkreis) ausgerich­tet bleiben!

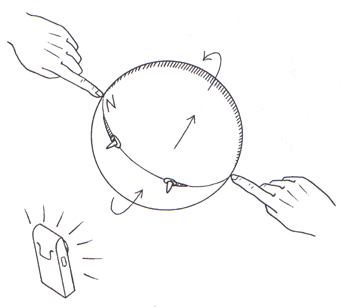
Abb. 8: Die Richtung des Schattens am Sonnenmittag ändert sich nicht, egal wie schräg man die "Erdachse" hält.

2. Unterrichtsstunde

Den Sonnenmittag in Alexandria und Syene reproduzieren

Da die beiden Städte nicht auf dem gleichen Längenkreis liegen (Alexandria liegt ca. 3 Grad weiter westlich als Syene; so weit liegen in Deutschland z. B. Braunschweig und Berlin, in Österreich Salzburg und Wien und in der Schweiz Genf und Sankt Gallen auseinander), gibt es für die Schüler neue Probleme zu lösen. Geben Sie jeder Gruppe die zurecht geschnittene Minikarte von Ägypten (siehe Materialliste ganz oben) und stellen Sie den Kindern eine neue Aufgabe: "Positioniert die Karte so auf dem Ball, dass ihr die Beobachtungen des Era­tosthenes zum Zeitpunkt des Sonnenmittags in Alexandria und in Syene nach­vollziehen könnt".

Nachdem die Schüler die beiden Schrauben auf die Minikarte geklebt haben, legen sie diese auf die von der Lampe beschienene Seite des Balls und ver­schieben sie so lange, bis der Schatten in Syene verschwindet. Dann befesti­gen sie den Kartenstreifen an allen vier Ecken an den Ball, wobei sie natürlich darauf achten müssen, dass die Nord-Süd-Achse der Karte in Richtung des Meridians ausgerichtet ist. Doch dann tritt ein Problem auf: Der Schatten in Alexandria zeigt nicht genau zum "Nordpol". Auch bei der Minikarte ist dies wegen des (absichtlich) zu groß gewählten Maßstabs deutlich erkennbar.

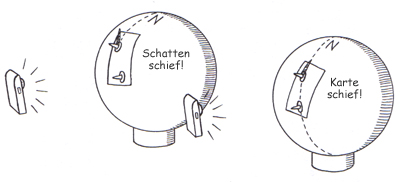
Abb. 9: Eine Komplikation: Alexandria und Syene liegen nicht auf dem gleichen Längenkreis!

Auf der Suche nach einer Lösung, drehen die Kinder den Ball etwas: Der Schatten zeigt jetzt nach "Norden" – und wird ein wenig kürzer – aber da taucht auch schon das nächste Problem auf: In Syene ist ein kleiner Schatten entstanden.

Sich an die vorhergehende Simulation erinnernd, versuchen einige Kinder beide Städte auf den auf dem Ball eingezeichneten "Längenkreis" zu legen. Und da­mit erreichen sie tatsächlich, dass der Schatten in Alexandria zum "Nordpol" zeigt und der in Syene verschwindet. Aber es gibt immer noch ein Problem: "Jetzt hängt die Karte schief!". Schlagen Sie den Kindern vor, die Karte wieder so zu drehen, dass sie "gerade" hängt. Sie sollen dabei aufmerksam die Bewe­gung der beiden Schatten von "Sonnenaufgang" bis zum "Sonnenmittag" beob­achten. Sie werden entdecken, dass es in Syene etwas früher "Sonnenmittag" ist als in Alexandria. Damit tut sich schon wieder ein Problem auf, denn das entspricht nicht dem historischen Text, in dem es heißt, dass die Beobachtun­gen des Eratosthenes zur gleichen Zeit gemacht worden sind. Aber um welche Art von Zeit handelte es sich überhaupt? Nicht um die Zeit auf unseren Uhren, die ja damals noch nicht erfunden waren, sondern um die von der Sonne ange­zeigte Zeit. Und die ist ja auf der Erde von einem Ort zum anderen verschie­den – genau so wie auf dem Ball. Die Kinder begreifen dann auch, dass die beiden Städte auf verschiedenen Längenkreisen liegen, und dass man auf einer Kugel unendlich viele Längenkreise einzeichnen könnte. Hierauf werden wir später noch zurückkommen.

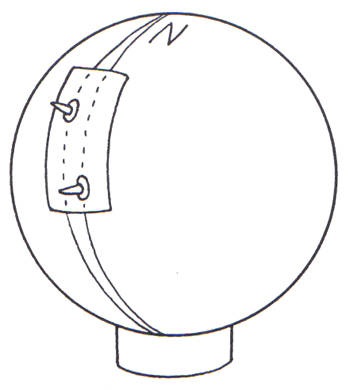
Abb. 10: So sieht es in Wirklichkeit aus, aber die Messung des Eratosthenes funk­tioniert trotzdem, wenn man genau zum jeweiligen Sonnenmittag misst.

Anmerkung: Falls es notwendig ist, erwähnen Sie (oder lassen Sie es die Schüler später ausrechnen), dass es in Alexandria fast eine Viertelstunde später Sonnenmittag ist als in Syene, dass aber dieser verhältnismäßig geringe Zeitunterschied Eratosthenes bei der Bestimmung des Erdumfangs kaum gestört hat.

Den Schülern wird spätestens jetzt bewusst, dass es in unserer modernen Welt nicht mehr möglich ist, sich nach der Sonnenzeit zu richten: In einem Land (zumindest in Europa, wo die Länder nicht allzu groß sind) gilt für das gesamte Territorium die gleiche Uhrzeit (sonst würden z. B. die Zugfahrpläne sehr, sehr kompliziert werden), und alle Länder der Erde müssen sich über ein System zur Festsetzung der so genannten gesetzlichen Zeit einigen (darauf kommen wir später noch zurück).

Mit dem von einer Taschenlampe angestrahlten Ball lässt sich auch die Verän­derung des Schattens eines "Mini-Gnomons" im Laufe der Jahreszeiten an­schaulich simulieren (siehe die bereits erwähnte fakultative Unterrichtseinheit "Die jahreszeitlichen Variationen des Schattens eines Gnomons simulieren").

© Sonnentaler/La main à la pâte | Impressum | Disclaimer | Datenschutz | RSS | E-Mail

© Sonnentaler / La main à la pâte  http://www.sonnentaler.net/