Die jahreszeitlichen Variationen des Schattens eines Gnomons simulieren (fakultativ)
| Publikation: | 3.4.2008 |
| Lernstufe: | 3 |
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Bei den hier vorgeschlagenen Simulationen geht es darum, die Entwicklung der Kurve, die die Spitzen der Gnomonschatten eines Tages miteinander verbindet, im Laufe der Jahreszeiten zu untersuchen. Bevor simuliert wird, sollten mehrmals im Laufe des Schuljahres Schattenverläufe aufgenommen worden sein (mindestens drei pro Halbjahr).
Simulation zum Zeitpunkt der Tagundnachtgleichen im Frühling (oder im Herbst)
In Anbetracht der Schattenverläufe, die im Herbst oder im Winter gemacht wurden und der darauf folgenden Simulationen, werden die Schüler vielleicht denken, dass die Kurvenform, die durch die Spitze des Schattens beschrieben wird, das umgekehrte Spiegelbild der durch die Sonne (oder die Lampe) beschriebenen Kurve ist. Diese neue Simulation wird ihnen beweisen, dass dem nicht so ist. Ideal ist es, wenn, vor dieser Simulation, am Tag der Tagundnachtgleichen (bzw. kurz vorher oder kurz nachher) sowie ca. zwei Wochen vorher jeweils ein Schattenverlauf aufgenommen wird, so dass die Schüler schon beobachten können, dass die Kurve langsam eine Gerade wird. (Wenn das – zum Beispiel weil es bewölkt ist – nicht klappen sollte, bereiten sie einfach ein Blatt Papier vor, auf das ein langer gerader Strich gezeichnet ist.) Wenn die Kinder dann wieder zu ihren Taschenlampen greifen, werden sie feststellen, dass diese "gezwungen" ist, eine Kurve zu beschreiben! (Und sie werden ahnen, dass die Geometrie, die dahinter steckt, nicht so einfach ist, wie es aussieht.)
Andererseits werden sie, wenn nach der Tagundnachtgleiche ein weiterer Schattenverlauf aufgenommen wird, beobachten können, wie die Kurve der Schattenspitzen sich entwickelt: Bitten Sie die Schüler, die Entwicklung der Kurvenform vorherzusagen, ihre Annahmen aufzuschreiben und sie natürlich zu gegebener Zeit zu überprüfen. Es ist sehr wahrscheinlich, dass zum Ende des Projektes hin einige Schüler ziemlich genau vorhersagen können, wie die Kurvenform sich im Laufe des Sommers und des Herbstes verändern wird: In den Ferien werden sie das natürlich nur dann überprüfen können, wenn sie sich zu Hause selbst ein Gnomon basteln. (Die folgende Abbildung gehört zur Abb. 12 der vorherigen Unterrichtseinheit "Aus Schattenfächern einen Sonnenkalender machen".)
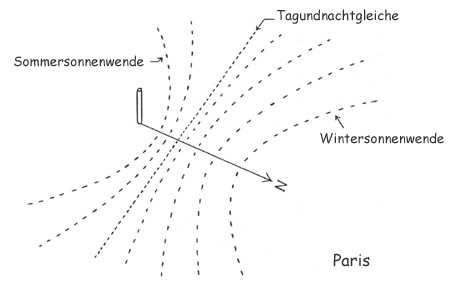
Abb. 13: Die Kurven die durch die Verläufe der Schatten zu verschiedenen Jahreszeiten gebildet werden
Die beiden Tagundnachtgleichen sind auch aus einem anderen Grund interessant, und zwar im Zusammenhang mit dem Winkel der Sonnenstrahlen zum Sonnenmittag und dem Breitengrad des Ortes. Falls ihre Schüler diese beiden Begriffe schon kennen und sie bereits diesen Winkel zu verschiedenen Zeitpunkten gemessen haben, werden sie feststellen, dass am Tag einer Tagundnachtgleiche dieser Winkel dem Breitengrad ihrer Schule entspricht!
An diesem Tag beleuchtet die Sonne die Erde nämlich auf ganz besondere Weise. Der kreisrunde Rand der von der Sonne beschienenen Taghälfte unseres Planeten geht an diesem Tag genau durch beide Pole. Ein Gnomon, den man auf der wahren Erde an einem dieser beiden Punkten unseres Planeten in die Erde stecken würde, hätte einen unendlich langen Schatten, da die einfallenden Sonnenstrahlen dort waagerecht zur Erdoberfläche sind, also ihr Winkel zur Erdoberfläche 90 Grad beträgt (was gerade dem Breitengrad der beiden Pole entspricht).
Umgekehrt fallen am Äquator die Sonnenstrahlen senkrecht auf den Gnomon (der also auch keinen Schatten werfen würde) und der Winkel ist Null, was dem Breitengrad des Äquators entspricht, nämlich 0 Grad. Genauso entspricht an allen anderen Orten der Erde an diesem Tag der Winkel der Sonnenstrahlen am Sonnenmittag dem Breitengrad des Ortes.
Simulation der jahreszeitlichen Veränderungen mit Hilfe eines Balls
Es sollte zuerst die Unterrichtseinheit "Simulation des Sonnenmittags mit Hilfe eines Balls" durchgenommen worden sein.
Auf einem von einer Taschenlampe beleuchteten Ball ist ein kleiner Gnomon aus Knete befestigt. Die Kinder machen sich ein Spiel daraus, mit einem Stift den Verlauf der Schattenspitze nachzuzeichnen, während der Ball langsam gedreht wird (der Ball wird durch Drehung des Sockels gedreht, wobei darauf geachtet werden sollte, dass der Sockel nicht seitlich verschoben wird). Sie vergleichen anschließend die erhaltene Kurve (1) mit denen, die sie bereits auf Pauspapier beim Nachzeichnen des Schattenverlaufs auf dem Schulhof aufgenommen haben. Sie überlegen sich, wie man eine dieser Kurven simulieren kann.
Es wird vorgegeben, dass weder die Lampe bewegt noch der Gnomon verschoben werden darf. Sie kommen schließlich darauf, dass man lediglich – in der Position des Sonnenmittags – den Ball leicht gegenüber der Lampe neigen muss. Und zwar entweder leicht nach vorn, um eine Sommerkurve zu erhalten (2), oder leicht nach hinten, um eine Winterkurve (3) zu erhalten.
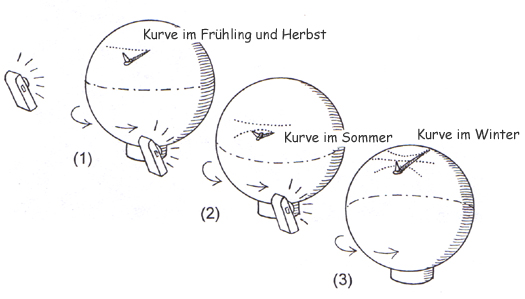
Abb. 14: Visiualisierung des Effekts des Kippens der Erde auf die Schattenverläufe
In Abb. 14 kann man mit Hilfe der Äquatorlinie dieses Kippen visualisieren: Aber wie ist das denn in Wirklichkeit? Kippt denn die Erde im Raum tatsächlich im Laufe eines Jahres? Eine sehr interessante Frage, die von den Kindern diesmal gelöst wird, indem sie einen Globus um einige im Kreis angeordnete Lampen (die die Sonne darstellen sollen) kreisen lassen. Sie werden feststellen, dass zum Beispiel auf der Höhe Deutschlands ein ähnlicher Effekt wie durch das Kippen des Balls erreicht werden kann, wenn die Erdachse immer parallel zu sich selbst bleibt, während sich die Erde um die Sonne bewegt.
Wenn die Achse sich zur "Sonne" hin neigt, ist es in Deutschland Sommer, und umgekehrt ist es Winter, wenn die Achse sich von der Sonne weg neigt. Die Kinder werden daraus natürlich sofort die Position des Globus' im Frühling und im Herbst folgern.
Letzte Aktualisierung: 29.11.2023






