7.3: Information binär kodieren
| Autoren: | |
| Publikation: | 8.12.2016 |
| Lernstufe: | 3 |
| Übersicht: | Die Schüler:innen erkunden, wie man mit dem Binärcode Information kodieren kann. |
| Angestrebte Kenntnisse: |
|
| Wortschatz: | kodieren, Bit, Binärcode |
| Dauer: | 1 Stunde 30 Minuten |
| Material: | Für jede:n Schüler:in: |
| Herkunft: | La main à la pâte, Paris |
Vorbemerkung
Wir ersetzen in dieser Unterrichtsstunde das Wort "verschlüsseln" durch das Wort "kodieren". Wenn man Zeichen nach einem allgemein bekannten Schema durch Nullen und Einsen ersetzt, wird meistens der Begriff "kodieren" verwendet.
Ausgangssituation
Die Lehrerin erklärt, dass elektronische Geräte in Wirklichkeit nicht direkt Zahlen übertragen können. Sie übertragen Lichtsignale oder elektrische Signale. Diese haben oft nur zwei Zustände: NEIN (kein Signal) oder JA (ein Signal). Man kann sich einen Kippschalter oder Schalthebel vorstellen, der entweder aus- oder eingeschaltet ist. Statt mit NEIN und JA bezeichnet man diese beiden Zustände oft mit 0 und 1. Die Schüler:innen müssen sich also eine neue Verschlüsselungsmethode ausdenken, die mit zwei Zeichen (0 und 1) auskommt. Die Ausgangsfrage lautet: "Wie kann man Information kodieren, wenn man nur Nullen und Einsen verwenden darf?".
Recherchearbeit: Strategien, um nur mit Nullen und Einsen zu kodieren
Die Lehrerin erinnert die Schüler:innen daran, dass der Rover von der Basisstation aus gesteuert wird, dass dafür aber nur die vier Wörter Norden, Süden, Osten und Westen verwendet werden dürfen. Die Schüler:innen überlegen sich eine Methode, wie man diese vier Wörter übermitteln kann, indem man nur Nullen und Einsen verwendet.

Abb. 1: Die Himmelsrichtungen kodieren [1]
Nach kurzer Zeit stellen die einzelnen Gruppen ihre Ideen vor. Sie vergleichen die verschiedenen Vorschläge und stellen fest: Da 0 und 1 nur zwei der vier Richtungen bezeichnen können, braucht man mehrstellige Binärzahlen.
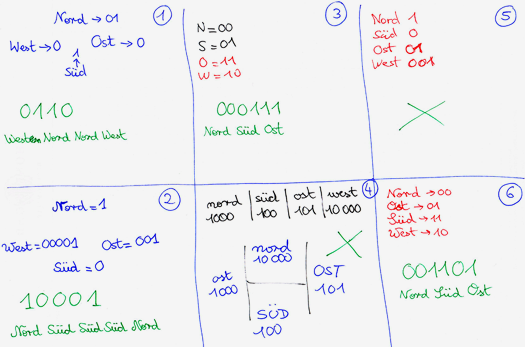
Abb. 2: Die Himmelsrichtungen kodieren – nicht alle Vorschläge funktionieren [1].
Pädagogische Anmerkungen
- Ein Vorschlag kann zum Beispiel darin bestehen, ...
- "Norden" durch "00" zu ersetzen,
- "Süden" durch "11",
- "Osten" durch "01" und
- "Westen" durch "10".
Hier wird jede Himmelsrichtung durch eine Dublette bestehend aus den Ziffern 0 oder 1 dargestellt. Jede mögliche Kombination von 0 und 1 kommt einmal vor. Die Gruppen, die sich für diese Methode entschieden haben, haben die verschiedenen Himmelsrichtungen wahrscheinlich anderen Dubletten zugeordnet als in obigem Beispiel geschehen. Alle Zuordnungen sind gleichberechtigt. -
Ein zweiter Vorschlag könnte darin bestehen, ...
- "Norden" durch "1000" zu ersetzen,
- "Süden" durch "0100",
- "Osten" durch "0010" und
- "Westen" durch "0001".
Hier wird jede Himmelsrichtung durch eine Folge von vier Ziffern (0 oder 1) dargestellt. Es werden nur wenige der möglichen Kombinationen verwendet (zum Beispiel wird 0000 nicht benötigt). -
Eine dritte Möglichkeit wäre die folgende Zuordnung:
Norden Süden Osten Westen 1
0 0
00
0 0
10
1 0
00
0 1
0
Die Idee hinter einem solchen Vorschlag ist gut, aber die Nullen und Einsen können nur nacheinander übertragen werden, das heißt ohne bestimmte Position im Raum. Wenn man die Ziffern hintereinander schreibt, entspricht dieser Vorschlag dem zweiten Vorschlag: Für jede Himmelsrichtung werden vier Ziffern gebraucht, eine Eins und drei Nullen. Es gibt vier verschiedene Möglichkeiten die 1 zu positionieren – eine Möglichkeit für jede Himmelsrichtung.
Aufgabe: Mit wie viel Nullen und Einsen kann man die Wochentage kodieren? (Gruppenarbeit)
Alle Nachrichten, die zwischen Basisstation und Rover hin- und hergeschickt werden, haben ein Datum. Man muss also zum Beispiel mit Nullen und Einsen übermitteln können, an welchem Wochentag die Nachricht geschrieben wurde. Die Schüler:innen sollen herausfinden, wie man die sieben Tage der Woche mit so wenig Nullen und Einsen wie möglich kodieren kann.
Gemeinsame Erörterung
Dafür reichen drei "0 oder 1". Dies ist eine Möglichkeit, aber es gibt zahlreiche Varianten:
- 000 für Montag
- 001 für Dienstag
- 010 für Mittwoch
- 011 für Donnerstag
- 100 für Freitag
- 101 für Samstag
- 110 für Sonntag
Es bleibt sogar eine Kombination übrig (in unserem Beispiel 111), die nicht benötigt wird.
Die Lehrerin verteilt das Arbeitsblatt 30 (Binärcode) und projiziert es parallel an die Wand. Die Klasse formuliert mit Hilfe der Lehrerin eine Zusammenfassung: "Man kann die Elemente einer Liste durch eine Aneinanderreihung von Nullen oder Einsen darstellen". Die 0 oder 1 heißen auch Bits – von Binary digits, was auf Deutsch Binärzahl heißt."
- Mit einem einzelnen Bit kann man zwei Elemente (oder Zeichen) kodieren: schwarz/weiß, ausgeschaltet/eingeschaltet zum Beispiel. Dem einen Element dieser Zweierliste ordnet man die "0", dem anderen die "1" zu. Die Schüler:innen notieren im Arbeitsblatt Beispiele für Listen mit zwei Elementen.
- Mit zwei hintereinandergeschriebenen Bits kann man bis zu vier Elemente kodieren, zum Beispiel Norden/Süden/Osten/Westen. Es gibt vier verschiedene Möglichkeiten, "0" und "1" zu kombinieren: "00", "01", "10" und "11". Die Schüler:innen notieren in das Arbeitsblatt Beispiele für Listen, die man mit zwei Bits (jedoch nicht mit einem Bit) kodieren kann. Diese Listen haben drei oder vier Elemente.
- Mit drei hintereinandergeschriebenen Bits kann man bis zu acht Elemente kodieren, zum Beispiel die sieben Tage der Woche. Es gibt in diesem Fall acht verschiedene Möglichkeiten, die Einsen und Nullen zu kombinieren: "000", "001", "010", "011", "100", "101", "110" und "111". Die Schüler:innen notieren in das Arbeitsblatt Beispiele für Listen, die man mit drei Bits (jedoch nicht mit zwei Bits) kodieren kann. Diese Listen haben 5, 6, 7 oder 8 Elemente.
- Je mehr Bits man kombiniert, desto mehr Elemente kann man darstellen: bis zu 16 Elemente mit 4 Bits, bis zu 32 Elemente mit 5 Bits, ... bis zu 256 Elemente mit 8 Bits usw. Schriftzeichen werden im Computer standardmäßig mit 8 Bits (= 1 Byte) kodiert.
Jede:r Schüler:in notiert in das Arbeitsblatt 30 (Binärcode) eine Liste von Elementen, die durch vier Bits kodiert werden, jedoch nicht durch drei Bits. Eine solche Liste hat zwischen 9 und 16 Elemente. Beispiele wären: die 12 Monate eines Jahres, die 10 Ziffern 0 bis 9, die 12 Stunden auf dem Ziffernblatt einer Uhr, die 10 Finger der beiden Hände, die Vornamen der 13 Cousins und Cousinen, 16 Namen von Tieren auf dem Bauernhof usw.
Aufgabe (in Zweiergruppen)
Die Lehrerin fragt die Schüler:innen, wie viele Bits man braucht, um die 26 Buchstaben des Alphabets zu kodieren. Die Schüler:innen überlegen ein paar Minuten. Bei der gemeinsamen Erörterung wird festgestellt, dass vier Bits nicht ausreichen (mit vier Bits lassen sich nur 2 x 2 x 2 x 2 = 16 Elemente kodieren). Fünf Bits reichen dagegen aus: Mit fünf Bits kann man 2 x 2 x 2 x 2 x 2 = 32 Elemente kodieren.
Zusammenfassung
Die Schüler:innen fassen zusammen, was sie in dieser Unterrichtsstunde gelernt haben.
Beispiel:
- Man kann die Elemente einer Liste (Himmelsrichtungen, Wochentage, Alphabet, ...) mit einer Reihe von Nullen und Einsen kodieren (verschlüsseln). Das nennt man Binärkodierung. Die Symbole 0 und 1 nennt man Bits.
- Je mehr Bits man hintereinander schreibt, desto mehr Elemente kann
man darstellen:
- Mit einem Bit kann man zwei Elemente darstellen,
- mit zwei Bits 2 x 2 = 4 Elemente,
- mit drei Bits 2 x 2 x 2 = 8 Elemente,
- mit fünf Bits 2 x 2 x 2 x 2 x 2 = 32 Elemente,
- mit acht Bits 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256 Elemente.
- Mit dem Binärcode kann man alle möglichen Daten darstellen, insbesondere Buchstaben und Zahlen.
- Ein Computer stellt jede Information im Binärcode dar.
Die Lehrerin vervollständigt das Plakat "Was ist Informatik?".
Mögliche Erweiterung (für die Sekundarstufe I)
In der Sekundarstufe I kann man den Schüler:innen auftragen, alle Kombinationsmöglichkeiten von "0" und "1" für zum Beispiel fünf Bits zu finden. Sie werden feststellen, dass es nicht so einfach ist, alle 32 Möglichkeiten zu finden, ohne einige davon zu wiederholen. Die Lehrerin schlägt ihnen dann vor, schrittweise vorzugehen.
- Bei einem Bit ist es einfach: 0, 1.
- Bei zwei Bits muss man nur zwei Mal die Liste für ein Bit abschreiben, ein Mal setzt man eine "0" davor, ein Mal eine "1": 00, 01, 10, 11.
- Bei drei Bits geht man analog vor: Man schreibt zwei Mal die Liste für zwei Bits ab, ein Mal setzt man eine "0" davor, ein Mal eine "1": 000, 001, 010, 011, 100, 101, 110, 111.
- Und so weiter und so fort.
Fußnote
1:
Abb. 1: 4. und 5. Klasse von Thyphaine Collignon (Vernaison)
Abb. 2: 5. Klasse von Christelle Crusberg (Champigny-sur-Marne)
Letzte Aktualisierung: 23.7.2025






