7.4: Nachrichten binär kodieren/dekodieren
| Autoren: | |
| Publikation: | 8.12.2016 |
| Lernstufe: | 3 |
| Übersicht: | Die Schüler:innen kodieren und dekodieren eine kurze Textnachricht. Sie verwenden dafür wieder den Binärcode. |
| Angestrebte Kenntnisse: |
|
| Wortschatz: | Bit, Binärcode |
| Dauer: | 1 Stunde |
| Material: | Für jede Gruppe: |
| Herkunft: | La main à la pâte, Paris |
Ausgangssituation
Die Basisstation hat geantwortet, dass ein Wirbelsturm im Anmarsch ist. Die Forscher:innen im Außeneinsatz sollen der Basisstation melden, wann sie voraussichtlich zurück sein werden. In dieser Unterrichtsstunde werden die Schüler:innen die Antwort an die Basisstation binär kodieren.
Recherchearbeit: Wie kann man eine Textnachricht binär kodieren?
Die Lehrerin erklärt, dass die Nachricht an die Basisstation nur Großbuchstaben, Leerzeichen und Punkte enthalten soll, insgesamt also 28 mögliche Zeichen. Sie fragt die Schüler:innen, wie viele Bits sie dafür brauchen werden. Sie erinnert sie eventuell an die vorherige Unterrichtsstunde und verweist auf das Arbeitsblatt 30 (Binärcode). Die Antwort lautet: Sie werden fünf Bits pro Buchstabe brauchen.
Die Lehrerin verteilt den oberen Teil des Arbeitsblattes 31 (Binär kodieren und dekodieren). Sie gibt den Schüler:innen fünf Minuten Zeit, um sich für eine Zuordnung zwischen Buchstabe und Gruppe von fünf Bits zu entscheiden. Bei der gemeinsamen Erörterung kann die Klasse zum Beispiel die folgende Zuordnung festlegen.
| 5 Bits | 00000 | 00001 | 00010 | 00011 | 00100 | 00101 | 00110 | 00111 |
|---|---|---|---|---|---|---|---|---|
| Zeichen | A | B | C | D | E | F | G | H |
| 5 Bits | 01000 | 01001 | 01010 | 01011 | 01100 | 01101 | 01110 | 01111 |
|---|---|---|---|---|---|---|---|---|
| Zeichen | I | J | K | L | M | N | O | P |
| 5 Bits | 10000 | 10001 | 10010 | 10011 | 10100 | 10101 | 10110 | 10111 |
|---|---|---|---|---|---|---|---|---|
| Zeichen | Q | R | S | T | U | V | W | X |
| 5 Bits | 11000 | 11001 | 11010 | 11011 | 11100 | 11110 | 11111 | 11111 |
|---|---|---|---|---|---|---|---|---|
| Zeichen | Y | Z | Punkt | Leerzeichen | können verwendet werden, um weitere Zeichen zu kodieren | |||
Tab. 1: Eine binäre Darstellung des Alphabets samt Punkt und Leerzeichen
Die Lehrerin verteilt die obige Zuordnungstabelle (siehe mittlerer Teil des Arbeitsblattes 31). Die Schüler:innen sollen mit Hilfe dieser Zuordnungstabelle folgende Nachricht binär kodieren:
ZEHN MINUTEN
| Buchstabe | Z | E | H | N | M | I | N | U | T | E | N | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 Bits | 11001 | 00100 | 00111 | 01101 | 11011 | 01100 | 01000 | 01101 | 10100 | 10011 | 00100 | 01101 |
Tab. 2: Binär kodierte Nachricht "ZEHN MINUTEN"
Aufgabe: Eine von der Basisstation gesendete Nachricht dekodieren (in Zweiergruppen)
Die Schüler:innen dekodieren die von der Basisstation gesendete Antwort (unterer Teil des Arbeitsblattes 31):
0111001010
Das Zerschneiden in 5er-Pakete ergibt: 01110 und 01010. Schaut man in der Zuordnungstabelle nach, entspricht dies den Buchstaben O und K. Diese Aktivität ist für die Schüler:innen sehr motivierend und festigt ihre Kenntnisse und ihr Verständnis der Binärkodierung (Binärverschlüsselung).
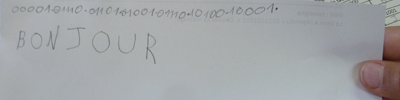
Abb. 1: Dekodieren einer Nachricht [1]
Zusammenfassung
Die Schüler:innen fassen zusammen, was sie in dieser Unterrichtsstunde gelernt haben.
Beispiel:
- Mit dem Binärcode kann man alle möglichen Daten darstellen, insbesondere Buchstaben und Zahlen.
Fußnote
1: Abb. 1: 4. Klasse von Carole Vinel (Paris)
Letzte Aktualisierung: 24.7.2025






