2.5: Die Schwalbe und der Frosch
| Autoren: | |
| Publikation: | 30.12.2017 |
| Lernstufe: | 3 |
| Übersicht: | Die Schüler lernen den Begriff der Korrelation kennen. Eine Korrelation ist ein ständig bestehender Zusammenhang zwischen zwei Ereignissen oder Merkmalen: Wenn sich das eine verändert, verändert sich auch das andere. Der Begriff der Korrelation ist grundlegend, um Ereignisse zu erklären und vorherzusagen. Die Schüler lernen Daten als Diagramm darzustellen und zu analysieren. |
| Angestrebte Kenntnisse: |
Wissenschaftlich denken, kritisch denken:
Die Erklärung eines Phänomens finden. Für Anfänger: Feststellen, dass es zwischen zwei Phänomenen Zusammenhänge gibt, die ein regelmäßiges Muster aufweisen (Korrelationen). Kompetenzen: Mit Unterstützung des Lehrers forschendes Lernen betreiben: Geeignete mathematische Werkzeuge verwenden; die für die Lösung des Problems nötigen Informationen erheben und sortieren (Texte, Tabellen, Diagramme, Zeichnungen, Schemata usw.) |
| Schwerpunkt: | Wissenschaft und Technik, Mathematik |
| Dauer: | 1 Stunde 30 Minuten (1 oder 2 Einheiten) |
| Material: | Für jeden Schüler oder jede Schülergruppe: Für jeden Schüler: |
| Herkunft: | La main à la pâte, Paris |
Aktivität: Korrelationen identifizieren
Ablauf: Die Schüler untersuchen zwei Tabellen: Die erste informiert über die Schwalbenpopulation (an einem Ort) an verschiedenen Tagen im Jahr. Die zweite beschreibt das Verhalten eines sogenannten Wetterfrosches in Abhängigkeit von der Luftfeuchtigkeit. Die Schüler stellen die Daten der beiden Tabellen als Diagramme dar und interpretieren diese (Phasen 1 und 2). Die Schüler stellen fest, dass man mit Hilfe eines Diagramms sichtbar machen kann, ob es zwischen zwei Ereignissen eine Korrelation gibt oder nicht (Phase 3). Sie machen sich Gedanken darüber, in welchen Alltagssituationen man es mit Korrelationen zu tun hat (Phase 4).
Botschaft zum Mitnehmen: Manchmal stellt man fest, dass es zwischen zwei Ereignissen (bzw. Merkmalen, Situationen, ...) einen Zusammenhang gibt: Wenn sich das eine Ereignis verändert, verändert sich auch das andere. So etwas nennt man eine Korrelation. Besteht eine Korrelation zwischen zwei Ereignissen, kann man anhand dieser Korrelation Vorhersagen machen. Aber Vorsicht vor allzu schnellen Schlüssen: Bevor man mit Sicherheit behaupten kann, dass eine Korrelation vorliegt, muss man viele Daten sammeln und analysieren. Nur dann kann man entscheiden, ob es sich bei einem beobachteten, regelmäßigen Muster um eine Korrelation handelt oder nicht. Stellt man Daten als Punktdiagramm dar, erkennt man eine Korrelation daran, dass sich die Datenpunkte praktisch auf einer Linie befinden [1].
Vorbemerkungen:
- In dieser Unterrichtseinheit machen sich die Schüler anhand der grafischen Darstellung eines Datensatzes mit dem Begriff der Korrelation vertraut. Haben die Schüler bisher keine Diagramme erstellt (Zeichnen einer Ausgleichsgeraden in einem Koordinatensystem), ist dies eine gute Gelegenheit, es anhand konkreter Daten zu lernen.
- Der Lehrer kann die Schüler das Diagramm selbst anfertigen lassen oder ihnen das fertige Diagramm aushändigen.
- Der Lehrer kann auch beschließen, den Schülern andere, ihm geeigneter erscheinende Daten zu geben.
Phase 1: Ausgangssituation
Der Lehrer schreibt das Sprichwort "Eine Schwalbe macht noch keinen Frühling" an die Tafel [2]. Was steckt hinter diesem Sprichwort? "Wenn man nur eine Schwalbe sieht, ist der Frühling noch nicht da?", "Erst wenn man viele Schwalben sieht, kann man sagen, dass es Frühling ist?" "Im Frühling kommen die Schwalben zahlreich [aus ihren Winterquartieren] zurück?"
Es gibt zahlreiche Sprichwörter, in denen das Verhalten eines Tieres oder eine bestimmte Beobachtung der Natur mit dem Wetter in Verbindung gebracht wird. Beispiele: "Abendrot – Gutwetterbot", "Morgenrot mit Regen droht", "Das Wetter am Siebenschläfertag [27. Juni] sieben Wochen bleiben mag", "Wenn im September die Spinnen kriechen, sie einen harten Winter riechen". Im Internet werden die Schüler unter dem Stichwort "Bauernregeln" zahlreiche weitere Beispiele finden. Nur wie steht es um den Wahrheitsgehalt dieser Bauernregeln? Gibt es wirklich einen Zusammenhang zwischen der Anzahl der Schwalben und dem Beginn des Frühlings? Kann man diese Aussage überprüfen? Stimmt dieses Sprichwort?

Abb. 1: Eine Rauchschwalbe und eine Mehlschwalbe
(links: Malene Thyssen,
Wikimedia Commons, CC BY-SA 3.0
rechts: C. Robiller, Wikimedia Commons,
CC BY-SA 3.0 DE)
Phase 2: Daten in einer Tabelle zusammenführen und als Diagramm darstellen (ca. 30 min)
Die Schüler schauen sich (jeder für sich, in kleinen Gruppen oder alle zusammen) das Arbeitsblatt 31 (Die Schwalben und der Frühling) an. In dem Arbeitsblatt ist eine Tabelle zu sehen – in der linken Spalte jeweils ein Datum, in der rechten die Anzahl der Schwalben, die an diesem Tag beobachtet wurden [3]. Die Schüler kommentieren die Tabelle: Zwischen April und Mai steigt die Schwalbenpopulation stark an. Im Februar und März wurden dagegen keine bzw. nur vereinzelt Schwalben gesichtet. Es scheint einen Zusammenhang zu geben zwischen der Anzahl der Schwalben und der Jahreszeit.
Die Schüler sollen nun die Daten der Tabelle grafisch darstellen. Eventuell kann der Lehrer vorgeben, dass das Datum auf der Rechtsachse aufgetragen wird und die Anzahl der Schwalben auf der Hochachse.
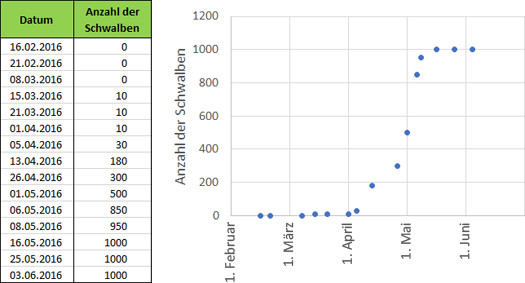
Abb. 2: Schwalbenzählung zwischen Februar und Anfang Juni 2016
Das Diagramm zeigt ganz deutlich, wie ab Anfang April die Anzahl der Schwalben stark ansteigt. Es besteht eindeutig ein Zusammenhang (eine Korrelation) zwischen der Anzahl der Schwalben (an diesem Ort) und der Jahreszeit. Der Zusammenhang erlaubt es uns, Vorhersagen zu machen: Wenn viele Schwalben zu sehen sind, kann man davon ausgehen, dass es Frühling ist.
Der Lehrer fragt: "Was ist Anfang März los?"Im März sieht man nur vereinzelt Schwalben, erst im April tauchen sie massenhaft auf. Die Erklärung für das Sprichwort "Eine Schwalbe macht noch keinen Frühling" könnte also sein: Wenn man einzelne Schwalben sieht, heißt es noch lange nicht, dass schon alle aus ihren Winterquartieren zurückgekehrt sind – das ist erst im Frühling der Fall.
Eine Korrelation ist ein ständig bestehender Zusammenhang zwischen zwei Variablen: Wenn sich die eine Variable verändert, verändert sich auch die andere. Wenn also zum Beispiel der Wert der einen Variablen größer wird, wird auch der Wert der anderen Variablen größer (positive Korrelation). Oder: Wenn der Wert der einen Variablen größer wird, wird der Wert der anderen Variablen kleiner (negative Korrelation).
Phase 3: Tabelle und zugehöriges Diagramm bei fehlender Korrelation der Variablen (ca. 30 min)
Die Schüler stellen die Daten der zweiten Tabelle als Diagramm dar. Dem Diagramm sollen sie entnehmen, ob eine Korrelation zwischen beiden Variablen besteht oder nicht. Sie lernen anhand der Art des Diagramms zu erkennen, ob eine Korrelation vorliegt oder nicht.
Der Lehrer liest den Schülern einen Text vor, der im 19. Jahrhundert von dem Zoologen Auguste Duméril, Professor am staatlichen Naturkundemuseum in Paris,geschrieben wurde.
Laubfrösche kündigen durch ihr Quaken Regen an. Man kann ein lebendes Hygrometer oder Barometer bauen, indem man eines dieser Tiere in ein Glasgefäß steckt. Versorgt man den Frosch gut mit Wasser und Insekten, kann man ihn sieben Jahre lang in so einem Glasgefäß halten. In diesem Gefängnis steht eine kleine Leiter. Klettert der Frosch die Leiter hoch, bedeutet das, dass das Wetter trocken bleibt.
Die armen Laubfrösche, die nur deswegen eingesperrt werden, um gutes oder schlechtes Wetter vorherzusagen! Aber können sie das Wetter wirklich vorhersagen? Gibt es wirklich einen Zusammenhang zwischen dem Wetter und dem Verhalten des Frosches?

Abb. 3: Alter Mann mit Wetterfrosch
(Quelle: Zeitschrift "Die Gartenlaube", 1887, Public Domain)
Die Schüler schauen sich das Arbeitsblatt 32 (Der Wetterfrosch) an (jeder für sich, in kleinen Gruppen oder alle zusammen). "Ein Forscher hat einen Frosch in einem Terrarium beobachtet. Er hat systematisch die Luftfeuchtigkeit gemessen und notiert, in welcher Höhe (über dem Boden des Terrariums) sich der Frosch aufhält. Erstellt aus den Daten der Tabelle ein Diagramm und untersucht, ob es eine Korrelation zwischen dem Verhalten des Frosches und der Luftfeuchtigkeit gibt."
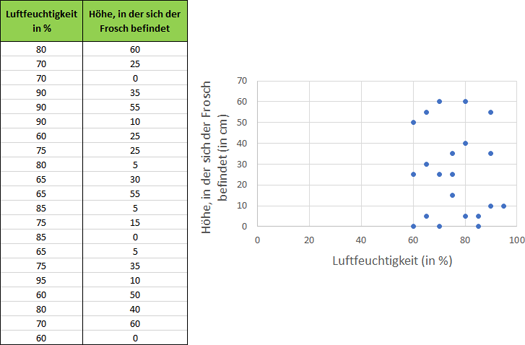
Abb. 4: Grafische Darstellung der Höhe, in der sich der Frosch im Terrarium aufhält, als Funktion der Luftfeuchtigkeit
Die Klasse diskutiert über das Diagramm. "Kann man irgendeine Tendenz erkennen? Halten sich die Frösche bei einer bestimmten Luftfeuchtigkeit immer in der gleichen Höhe auf?" Die Klasse stellt fest, dass dem nicht so ist. Steigt die Luftfeuchtigkeit an, kann man nicht sagen, ob der Frosch in seinem Terrarium mehr oder weniger nach oben klettert. Es gibt keinen Zusammenhang – keine Korrelation – zwischen diesen beiden Tatsachen.
Der Lehrer bittet die Schüler nun die beiden Diagramme zu vergleichen: das mit dem Frosch (keine Korrelation vorhanden) und das mit den Schwalben (Korrelation vorhanden): "Was fällt euch bei der Verteilung der Datenpunkte im Diagramm auf?" In dem Schwalben-Diagramm sieht man ab Anfang April eine "Linie nach oben gehen", während man im Frosch-Diagramm nichts Besonderes erkennt, außer einer Wolke von Datenpunkten. Man kann also einem Diagramm ansehen, ob eine Korrelation vorliegt oder nicht.
Die Klasse zieht folgenden Schluss zum Wetterfrosch: "Es ist nicht sinnvoll, einen Frosch in ein Gefäß zu sperren, um die Luftfeuchtigkeit vorherzusagen!" Laubfrösche sind keine guten Indikatoren (Wetterindikatoren in diesem Fall).
Wissenschaftliche und historische Anmerkung
In der Volksweisheit gibt es zahlreiche Legenden über die angebliche Fähigkeit von Tieren, das Wetter vorherzusagen. Die Legende mit dem "Wetterfrosch" im Glas ist eine davon. Früher gab es noch keine präzisen Instrumente zur Messung des Luftdrucks (der eng mit dem Wetter zusammenhängt). Für die Feldarbeit hatten die Menschen aber natürlich damals schon das Bedürfnis, das Wetter vorhersagen zu können.
Dass man für die Wettervorhersage den Laubfröschen vertraute, lag an der folgenden Beobachtung: Laubfrösche klettern auf Bäume (bis in hohe Äste), um Insekten zu fangen. Bei feuchter Luft fliegen Insekten in geringer Höhe über dem Boden, bei trockener Luft dagegen (auch) weiter oben. Das kann natürlich das Verhalten der Frösche beeinflussen – aber nicht in einem Glasgefäß, in dem die Frösche mit toten Insekten gefüttert werden. Der Legende des Wetterfrosches liegen also falsch interpretierte Beobachtungen zugrunde.
Zusammenfassung
Im Alltag nehmen wir regelmäßige Muster schnell wahr und interpretieren sie. Wir nehmen uns aber oft nicht die Zeit, zu überprüfen, ob unsere Interpretation richtig oder falsch ist.
Im Rahmen einer gemeinsamen Diskussion erwähnt die Klasse Alltagssituationen, in denen man auf den ersten Blick den Eindruck hat, dass zwei Phänomene miteinander zusammenhängen. Sie überlegen sich, welche dieser "Zusammenhänge" sie gern wissenschaftlich überprüfen würden. Beispiele: "Ich habe den Eindruck, dass jedes Mal, wenn ich im Haus meinen Regenschirm aufspanne, es im Laufe des Tages regnet." Oder: "Ich habe den Eindruck, dass alle Leute, die joggen gehen, gesünder sind." Oder: "Meine Mutter sagt, dass man sich im Winter weniger oft erkältet, wenn man jeden Morgen Vitamin C zu sich nimmt."
Die Klasse diskutiert über mögliche Tests, mit denen man solche Behauptungen überprüfen könnte. Es sei dabei an die Schwalbe erinnert, die noch keinen Frühling macht: Aus einer einzigen Beobachtung kann man keine Schlussfolgerung ziehen. Man muss viele Daten sammeln und mathematische Werkzeuge benutzen (zum Beispiel das Erstellen von Diagrammen), um zu sehen, ob sich Tendenzen abzeichnen. Besteht eine regelmäßige Verknüpfung zwischen zwei Variablen (Ereignissen, Merkmalen, Größen), kann man Vorhersagen machen. Außerdem erhält man dadurch einen Hinweis auf die kausale Erklärung.
Evaluation
Jeder Schüler bekommt den Evaluationsbogen 17 (Ein Diagramm interpretieren), in dem ein Diagramm interpretiert werden soll. Die Schüler müssen die Variablen identifizieren und herausfinden, ob es einen korrelativen Zusammenhang gibt. Diesmal müssen die Schüler ein Diagramm lesen (und interpretieren), und nicht selbst erstellen.
Es geht um die Schuhgröße (Rechtsachse) und die Anzahl der Fehler, die eine Person im Diktat macht (Hochachse) – siehe auch die Unterrichtseinheit 2.6 (Die vermeintliche Ursache). Diese Evaluation kann also als Einführung in die nächste Unterrichtseinheit dienen.
Fußnoten
1: Oft ist der Zusammenhang linear, aber nicht immer. Ist der Zusammenhang linear, liegen die Datenpunkte auf einer ansteigenden (positive Korrelation) oder einer abfallenden Gerade (negative Korrelation).
2:
Oft lautet das Sprichwort auch "Eine Schwalbe macht noch keinen Sommer".
Ob Frühling oder Sommer, die Bedeutung ist in beiden Fällen gleich:
"Man sollte keine voreiligen Schlüsse ziehen."
Das Sprichwort (eigentlich wäre "das geflügelte Wort" die richtigere Bezeichnung)
stammt aus der Fabel "Der verschwenderische Jüngling und die Schwalbe"
des griechischen Dichters Äsop. Dort heißt es: "Eine Schwalbe macht noch
keinen Frühling". Auch in anderen Sprachen kommt mal der Sommer vor
(etwa im Englischen: "A swallow does not make a summer")
oder der Frühling (etwa im Französischen: "Une hirondelle
ne fait pas le printemps"). Wir verwenden hier die Version mit dem
Frühling, weil sie besser in den Kontext der Unterrichtseinheit passt:
In unseren Breiten (Mitteleuropa) kommen die Schwalben im Frühling an.
3: Diese Schwalbenzählung haben Hobby-Vogelbeobachter in Frankreich gemacht.
Vögel beobachten: Vögel der Schweiz, Euro-Bird-Portal, NABU-Naturgucker
Letzte Aktualisierung: 4.11.2024






