2.6: Die vermeintliche Ursache

Autoren:
Publikation:	21.12.2017
Lernstufe:	3
Übersicht:	Die Schüler lernen zwischen tatsächlichem Kausalzusammenhang und scheinbarer Korrelation zweier Faktoren zu unterscheiden. Wer den Unter­schied nicht erkennt, wird falsche Schlüsse ziehen.
Angestrebte Kenntnisse:	Wissenschaftlich denken, kritisch denken: Die Erklärung eines Phäno­mens finden. Für Fortgeschrittene: Sich dessen bewusst sein, dass es einen Zusammen­hang zwischen zwei Dingen geben kann, dieser Zusammenhang aber nicht zwangsläufig kausal sein muss. Kompetenzen: Mit Unterstützung des Lehrers forschendes Lernen betrei­ben: Geeignete mathematische Werkzeuge verwenden; die für die Lösung des Problems nötigen Informationen erheben und sortieren (Texte, Tabellen, Diagramme, Zeichnungen, Schemata usw.)
Schwerpunkt:	Wissenschaft und Technik, Mathematik
Dauer:	Aktivität 1: 1 Stunde 30 Minuten (2 Einheiten) Aktivität 2: 2 Stunden 45 Minuten (mindestens 3 Einheiten)
Material:	Für die Klasse oder für jede Schülergruppe: das Arbeitsblatt 33: "Das geheimnisvolle Diagramm" Projektionsmöglichkeiten, um den Schülern das Video von Albert Michotte zu zeigen Fotoapparat oder Handy mit Kamerafunktion, um Bilder zu machen zwei Murmeln unterschiedlicher Farbe Für jeden Schüler: den Evaluationsbogen 18: "Gibt es einen Zusammenhang?"
Herkunft:	La main à la pâte, Paris

Aktivität 1: Was hat die Fußgröße mit der Anzahl der Fehler in einem Diktat zu tun?

Ablauf: Die Schüler untersuchen ein Diagramm, in dem ein Zusammenhang zwischen zwei Größen zu erkennen ist. Man nennt so etwas eine Korrelation zwischen zwei Variablen (Phase 1). Die Schüler erheben und analysieren in ihrer Klasse Daten zur Fußgröße der Schüler und zur Anzahl der Fehler, die sie im Diktat machen (Phase 2). Mit Hilfe des Lehrers lernen sie zwischen korre­lativem und kausalem Zusammenhang zu unterscheiden (Phase 3). Sie über­tragen ihre Überlegungen auf Situationen in der Wissenschaft und im Alltag (Phase 4).

Botschaft zum Mitnehmen: Wenn man feststellt, dass zwei Tatsachen zusammenhängen, muss man entscheiden können, ob es sich um einen kausalen Zusammenhang handelt oder um einen anderen Zusammenhang.

Vorbemerkungen:

• In dieser Unterrichtseinheit wird die grafische Darstellung eines Datensat­zes analysiert. Die Schüler sollten im Mathematikunterricht (bzw. im NaWi- oder Physikunterricht) bereits das Arbeiten mit Diagrammen gelernt haben, oder die Unterrichtseinheit "Die Schwalbe und der Frosch" durchgenommen haben.
• Der Lehrer kann die Schüler das Diagramm selbst anfertigen lassen oder ihnen das fertige Diagramm aushändigen.
• Der Lehrer kann auch beschließen, den Schülern ein anderes Diagramm zu geben, das er selbst erstellt hat und das ihm geeigneter erscheint.

Phase 1: Ein Diagramm interpretieren (ca. 15 min)

Der Lehrer gibt den Schülern das Arbeitsblatt 33 (Das geheimnisvolle Diagramm). Die in Gruppen aufgeteilten Schüler schauen sich das Arbeitsblatt genauer an. Anschließend wird das Arbeitsblatt mit der ganzen Klasse erörtert. Das Diagramm wird beschrieben: Es werden die Achsen identifiziert und die beiden Größen (Variablen). "Das Diagramm zeigt, wie die Anzahl der Fehler, die ein Schüler im Diktat macht, mit seiner Fußgröße zusammenhängt." Es scheint zwischen beiden Größen (Anzahl der Fehler und Fußgröße) eine kausale Beziehung zu geben: Hat der Schüler größere Füße, macht er weniger Fehler im Diktat.

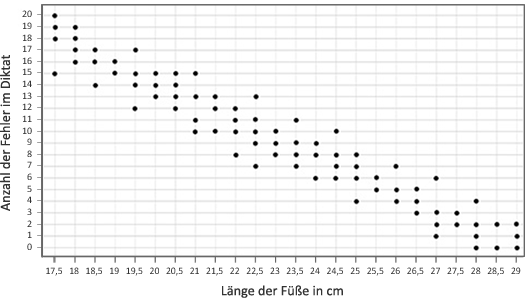
Abb. 1: Anzahl der Fehler im Diktat als Funktion der Fußgröße

Phase 2: Daten sammeln, in einer Tabelle zusammenführen und als Diagramm darstellen (ca. 30 min)

Der Lehrer erläutert: "Wir könnten in der Klasse eine ähnliche Erhebung machen und von jedem Schüler die Schuhgröße sowie die Anzahl der Fehler, die er im Diktat gemacht hat, in eine Tabelle schreiben. Anschließend könntet ihr das dazugehörige Diagramm zeichnen. Denkt ihr, dass ein ähnlicher Zusammenhang herauskommen würde wie der in Abbildung 1?" Der Lehrer bittet die Schüler, sich zu überlegen, wie sie die entsprechenden Daten erheben würden. Beispiel:

• Jeder Schüler misst mit einem Lineal die Länge seiner Füße. Oder er notiert seine Schuhgröße auf einen kleinen Zettel.
• Der Lehrer lässt die Schüler ein Diktat schreiben. Die Anzahl der Fehler wird auf denselben Zettel geschrieben – anonym, um die Schüler nicht bloßzustellen.
• Die Zettel werden gefaltet, eingesammelt und ausgezählt. Die Daten werden an der Tafel in eine zweispaltige Tabelle übertragen, oder auf ein Blatt Papier, das der Lehrer anschließend für jeden Schüler oder jede Schülergruppe fotokopiert.

Die Schüler erstellen (in Einzel- oder Gruppenarbeit) aus den Daten ein Dia­gramm. Auf der Rechtsachse wird die Fußgröße aufgetragen, auf der Hoch­achse die Anzahl der Fehler im Diktat. Die Daten werden durch Punkte oder Kreuze dargestellt. Falls Schüler mit gleicher Fußgröße gleich viele Fehler im Diktat gemacht haben, werden sich die entsprechenden Datenpunkte über­lagern.

Phase 3: Unterscheiden zwischen korrelativem und kausalem Zusam­menhang (ca. 15 min)

Die Klasse vergleicht ihr "eigenes" Diagramm mit dem Diagramm aus Abb. 1. "Sind die beiden Diagramme vergleichbar?" Meistens sieht das mit den Daten der Klasse gewonnene Diagramm anders aus, da die Schüler eines Jahrgangs in der Regel ähnlich große Füße haben.

"Wie kommt es, dass der Zusammenhang nicht der gleiche zu sein scheint?" Die Schüler antworten zum Beispiel: "Vielleicht haben die Forscher – um dieses Diagramm zu erhalten – Kinder und Erwachsene ein Diktat schreiben lassen. In diesem Fall ändert sich nicht nur die Fußgröße, sondern auch das Alter. Erwachsene haben größere Füße und sie kennen sich besser mit der Rechtschreibung und der Grammatik aus. Sie machen daher weniger Schreib­fehler."

Wenn die Schüler keine Erklärung haben, kann der Lehrer ihnen auf die Sprün­ge helfen: "Wird man, wenn man große Füße hat, besser in Rechtschreibung und Grammatik? Ist Letzteres eine Folge der großen Füße?" Die Diskussion soll die Schüler darauf bringen, dass das Alter eine verborgene Ursache ist, mit der man das Ergebnis von Abb. 1 erklären kann: Sowohl die Fußgröße als auch das Beherrschen der Rechtschreibregeln nehmen mit dem Alter zu. Es liegt also an der gemeinsamen Ursache – dem Alter –, dass es einen Zusammenhang zwi­schen der Fußgröße und der Anzahl der Fehler im Diktat gibt.

Damit die Schüler das gut verstehen, kann der Lehrer es ihnen anhand der Abb. 2 erläutern.

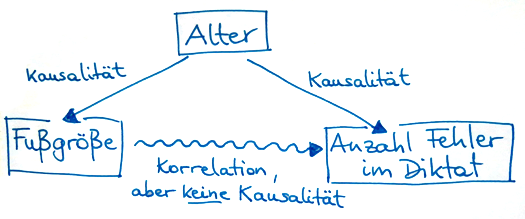
Abb. 2: Schema zur Erklärung des Unterschieds zwischen Kausalität und Korrelation

Aktivität 2: Vortäuschung einer vermeintlichen Ursache

Ablauf: Der Lehrer zeigt den Schülern ein Video von Albert Michotte. In dem Video ist eine kurze Animation zu sehen, mit der das Phänomen der "Illusion einer Kausalitätsbeziehung" verdeutlicht wird. Die Schüler analysieren die Animation und zählen die Gründe (Parameter) auf, die zu der Illusion führen (Phase 1). Der Lehrer kann die Schüler selbst solch eine vermeintliche Ursache konstruieren lassen (Phasen 2 und 3). Oder er lässt sie sofort Alltagsbeispiele mit vermeintlichen Ursachen suchen – Situationen, in denen man "etwas zu schnell" auf eine Ursache-Wirkungs-Beziehung (eine Kausalitätsbeziehung) tippt, obwohl es sich in Wirklichkeit um zwei unabhängige Ereignisse handelt (Phase 4).

Botschaft zum Mitnehmen: Wenn zwei Ereignisse kurz hintereinander auf­treten, neigen wir manchmal voreilig dazu, sie als "Ursache" und "Wirkung" zu deuten. Das zuerst auftretende Ereignis ist vermeintlich die Ursache, das zweite die Wirkung. Das kann aber eine Illusion sein.

Vorbemerkung: In dieser Aktivität wird eine Animation untersucht. Anschlie­ßend produzieren die Schüler selbst Animationen, in denen die Illusion einer Kausalitätsbeziehung erzeugt wird. Falls die Schüler bereits selbst program­miert haben (zum Beispiel mit Scratch [1]), können sie selbst eine solche Animation erstellen. Wenn nicht, können sie auch einfach ein Daumenkino basteln oder eine Bilderreihe aufnehmen und diese auf dem Computer oder dem Smartphone rasch abspielen (schnelle Diashow).

Phase 1: Eine Animation beschreiben und analysieren (ca. 15 min)

Der Lehrer zeigt den Schülern das folgende Video (von 1940). Darin ist ein Experiment des Psychologen Albert Michotte zu sehen:

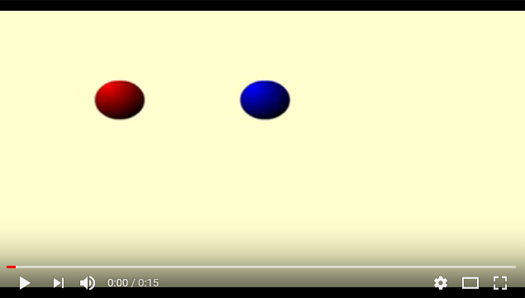
Abb. 3: Video eines Experiments von Albert Michotte

Die Schüler beschreiben die kleine Animation und machen Kommentare: "Man sieht zwei Murmeln. Die rote nähert sich der blauen und es sieht so aus, als würde die rote Murmel mit der blauen zusammenstoßen. Dann bewegt sich die blaue Murmel. Man könnte also meinen: Die Bewegung der roten Murmel ist die Ursache für die Bewegung der blauen Murmel." Es gibt allerdings keine Anhaltspunkte dafür, dass es sich hier um eine kausale Beziehung handelt. Es sind lediglich zwei geometrische Figuren zu sehen, die sich im Raum bewegen. Diese Animation ist ein klassisches Beispiel für eine Kausalitätsillusion.

Welches sind die Elemente, die uns denken lassen, dass die Bewegung der ersten Murmel die Ursache für die Bewegung der zweiten Murmel ist? Die Schüler erwähnen vielleicht: die Bewegungsrichtung der beiden Murmeln, der Eindruck eines Zusammenstoßes der beiden Murmeln, die Zeitverzögerung zwischen dem Zusammenstoß und der Bewegung der zweiten Murmel. Ein fundamentales Kriterium ist die Zeit: Man betrachtet im Allgemeinen die Bewegung der ersten Murmel als Ursache für die Bewegung der zweiten Murmel.

Phase 2 (optional): Eine Kausalitätsillusion erzeugen (ca. 1 Stunde)

Der Lehrer vertraut jeder Schülergruppe einen Fotoapparat (bzw. ein Smart­phone oder einen Tabletcomputer) an. Sie bekommen auch zwei verschieden­farbige Murmeln. Die Aufgabe lautet: "Ihr sollt nun die Kausalitätsillusion von Michotte reproduzieren. Platziert dazu die beiden Murmeln auf den Tisch und fotografiert sie. Verändert leicht ihre Position und macht erneut ein Foto. Wiederholt diesen Schritt, bis ihr die gesamte 'Bewegung' fotografiert habt."

Schaut man sich anschließend die Fotos in rascher Abfolge an, sieht es so aus, als würden sich die Murmeln bewegen ("Stop-Motion"). Bei dieser Gele­genheit kann die Klasse erneut über die Gründe (Parameter) diskutieren, die eine Kausalitätsillusion verursachen.

Phase 3 (optional): Eine Kausalitätsillusion zerstören (ca. 1 Stunde)

Die Schüler benutzen das Material aus Phase 2 und lösen eine weitere Auf­gabe: "Zerstört die Kausalitätsillusion!" Dazu wählen die Schüler einen der in Phase 1 aufgezählten Parameter (Gründe) und verändern diesen. Zum Beispiel: Die erste Murmel bleibt stehen, bevor sie mit der zweiten Murmel "zusammen­stößt"; die erste Murmel bewegt sich kaum, aber die zweite setzt sich trotz­dem in Bewegung; die Abfolge der Bewegungen wird umgekehrt (Film rück­wärtslaufen lassen); lange Pause zwischen den beiden Bewegungen usw. Es sollte immer nur ein Parameter auf einmal geändert werden.

Die Schüler stellen sich gegenseitig ihre Animationen vor und diskutieren gemeinsam darüber. In allen Fällen gilt: Wenn einer der Parameter verändert wird, verschwindet die Kausalitätsillusion. Einige der Parameter scheinen jedoch für die Illusion wichtiger zu sein als andere. Wenn die zeitliche Abfolge beibehalten wird (Bewegung 1 geschieht vor Bewegung 2), kommen nach wie vor Zweifel auf, ob es nicht vielleicht doch einen kausalen Zusammenhang gibt. Es ist wirklich sehr verlockend, einen kausalen Zusammenhang zwischen zwei Ereignissen zu sehen, wenn beide Ereignisse direkt nacheinander geschehen.

Phase 4 (optional): Kausalitätsillusionen in unserem Alltag (ca. 30 min)

Die Klasse sollte jetzt verstanden haben, dass die Tatsache, dass ein Ereignis vor einem anderen stattfindet, nicht zwangsläufig bedeutet, dass es zwischen beiden einen kausalen Zusammenhang gibt (dass das erste die Ursache für das zweite ist). Die Schüler sollen nun nach Alltagsbeispielen suchen, die Kausali­tätsillusionen sind. Sie können auch plausible Beispiele erfinden.

• "Seitdem Jan gekommen ist, läuft alles schief. Jan ist für all das Unheil verantwortlich."
• "Seitdem der Bus durch unsere Straße fährt, schmeckt das Leitungs­wasser nicht mehr. Der Bus ist die Ursache für das schlecht schme­ckende Wasser."
• "Vor einem Monat habe ich angefangen Blaubeeren zu essen, und seit­dem habe ich in der Schule exzellente Noten. Ich muss unbedingt weiter Blaubeeren essen."
• "Der Hahn kräht vor dem Sonnenaufgang. Der Hahn macht, dass die Sonne aufgeht."
• "Als Tim (von Tim und Struppi) zu den Incas kommt, gibt es eine Sonnen­finsternis. Die Incas glauben, dass Tim die Sonnenfinsternis verursacht hat."
• "Ich habe eine Person vorbeirennen sehen. Dann kam eine zweite Person vorbeigerannt. Die zweite hat bestimmt die erste verfolgt."

Die Klasse diskutiert über die Auswirkung von Kausalitätsillusionen auf unseren Alltag. Man sollte vorsichtig sein und Situationen nicht voreilig falsch interpre­tieren. Auch unser Verhalten sollte nicht auf unbegründeten Gründen beruhen (es wäre z. B. völlig falsch, Jan aus der Klasse zu nehmen).

Zusammenfassung

Der Lehrer bringt die Schüler dazu, über Alltagsbeispiele nachzudenken (zum Beispiel Nachrichten im Fernsehen, Behauptungen in einer Werbung usw.), bei denen man den Eindruck hat, es handele sich um zwei kausal zusammenhän­gende Ereignisse – dabei sind es lediglich zwei Ereignisse, die durch ein regel­mäßiges Muster miteinander verknüpft sind. Für jedes dieser Beispiele kann man ein Schema, wie das von Abb. 2 zeichnen. Wenn den Schülern spontan keine Beispiele einfallen, kann der Lehrer welche vorschlagen und die Schüler die Beispiele kommentieren lassen.

Beispiel 1: "In der Werbung wird immer wieder behauptet, dass Personen, die hochwertige Lebensmittel konsumieren (Olivenöl zum Beispiel, oder Voll­kornprodukte) gesünder und länger leben. Kann man daraus schlussfolgern, dass diese Lebensmittel die Ursache für ihre bessere Gesundheit sind?" Oft steckt hinter solchen Behauptungen eine versteckte Variable: das sozioöko­nomische Niveau, das es der Person erlaubt, einen in mehrerer Hinsicht gesün­deren Lebensstil zu führen, der sich natürlich auch auf die Gesundheit und die Langlebigkeit auswirkt.

Beispiel 2: "Man sagt, dass Kinder, die gewalthaltige Spiele spielen, gewalt­tätiger sind. Sind es zwingenderweise die Spiele, die sie gewalttätiger ma­chen?" Man kann anhand der Korrelation zwischen gewalthaltigen Spielen und gewalttätigem Verhalten keine Aussage treffen. Vielleicht suchen sich gewalt­tätige Kinder auch gewalthaltige Spiele aus.

Beispiel 3: "Wenn einem kalt ist, wird man krank." Eine Erkältung (ein grippa­ler Infekt) wird durch ein Virus verursacht. Zwischen Krankheit und Kälte gibt es eine Korrelation aber nicht unbedingt einen kausalen Zusammenhang. Erkältungen treten im Winter, also wenn es kalt ist, öfter auf. Der Grund ist aber eher, dass man sich mehr in geschlossenen Räumen aufhält, und das die Verbreitung der Viren begünstigt. Außerdem ist einem, wenn man krank ist, schneller kalt. In diesem Fall ist der kausale Zusammenhang umgekehrt: Weil man krank ist, friert man.

Es können auch Beispiele aus dem Bereich des Aberglaubens erwähnt werden. Zum Beispiel: "Wenn eine schwarze Katze die Straße überquert, geschieht ein Unglück." Verursacht die schwarze Katze das Unglück? Stimmt es überhaupt, dass es einen Zusammenhang zwischen diesen beiden Variablen gibt? Oft sehen wir Ursachen, die es gar nicht gibt, und Zusammenhänge (Korrelatio­nen), die keine sind. Man müsste nur zählen, wie oft nichts passiert, wenn eine schwarze Katze die Straße überquert. Das fällt uns aber weniger auf als ein negatives Ereignis – wir bemerken es einfach nicht.

Die Klasse denkt nun darüber nach, welche Auswirkungen solche vermeintli­chen Zusammenhänge (und seien sie noch so abstrus) auf unsere Entschei­dungsprozesse haben. Wenn sie zum Beispiel für einen kommerziellen Zweck eingesetzt werden, um uns zu überzeugen oder uns Angst zu machen, sollten wir da nicht vorsichtig sein?

Zum Schluss diskutiert die Klasse über die grundlegende Bedeutung des Unter­schieds zwischen korrelativem und kausalem Zusammenhang im Kontext der Forschung. In der Medizin zum Beispiel reicht es nicht aus zu wissen, dass Personen durch die Einnahme eines bestimmten Medikaments gesund werden. Man muss sicher sein, dass es wirklich an dem Medikament liegt, dass die Person wieder gesund wird. Erkältungen dauern in der Regel sieben Tage. Nimmt man ein Medikament gegen Erkältung, wird man in sieben Tagen gesund. Man könnte daher meinen, dass das Medikament eine positive Wirkung hatte. Aber in Wahrheit hängt die Gesundung nicht mit der Einnahme des Medika­ments zusammen, sondern mit dem natürlichen Verlauf einer Erkältung. Wie stellen es Wissenschaftler in solch einem Fall an, um herauszufinden, ob ein kausaler oder lediglich ein korrelativer Zusammenhang besteht? Sie führen Experimente durch, in denen alle Variablen kontrolliert werden und in denen es keine verborgenen Variablen gibt.

Evaluation

Für die Aktivität 1: Jeder Schüler bekommt den ersten Teil des Evaluations­bogens 18 (Gibt es einen Zusammenhang?), in dem sie ein Diagramm interpre­tiert werden sollen. "Handelt es sich um eine Korrelation oder um einen kau­salen Zusammenhang? Welches sind die Variablen? Welche Variable könnte die verborgene Variable sein?" Mit dieser Aufgabe kann evaluiert werden: 1. in­wiefern die Schüler in der Lage sind, zwischen einer Korrelation und einer Ursache-Wirkungs-Beziehung zu unterscheiden; 2. ob sie die richtigen Hin­weise und Argumente für die Existenz einer verborgenen Variablen finden; 3. ob sie ein Diagramm interpretieren können, das eine Korrelation darstellt.

Für die Aktivität 2: Im zweiten Teil des Evaluationsbogens 18 (Gibt es einen Zusammenhang?) sollen die Schüler "ihrer Großtante" erklären, dass wenn sich A vor B ereignet, das nicht unbedingt bedeutet, dass A die Ursache von B ist. Es geht wieder um einen Aberglauben (die Großtante ist der Meinung, dass man beim Würfeln ein gutes Ergebnis erzielt, wenn man vor dem Würfeln über die Würfel pustet). Die Schüler können zum Beispiel einen einfachen Versuch planen, wie man den Wahrheitsgehalt dieser Aussage überprüfen könnte. Zum Beispiel könnte man mehrmals würfeln – einmal mit und einmal ohne Pusten.

---

Fußnote

1: Siehe zum Beispiel "Erste Programmierschritte mit Scratch" aus dem Unter­richtsmodul "1, 2, 3 ... kodiert, programmiert, verschlüsselt!".

© Sonnentaler/La main à la pâte | Impressum | Disclaimer | Datenschutz | RSS | E-Mail

© Sonnentaler / La main à la pâte  http://www.sonnentaler.net/