Hilfestellungen zur Projektphase 4: Die Messungen verbessern und ihre Genauigkeit abschätzen

Publikation:	27.10.2007
Lernstufe:	3
Herkunft:	La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos

Um den Austausch der Messwerte zwischen den verschiedenen Schulen zu optimieren, werden die Teilnehmer des Projektes so gruppiert, dass die Brei­tengraddifferenz zwischen den Schulen einer Gruppe groß genug ist. Das heißt, dass in einer Gruppe mindestens eine andere Schule ist, deren Breitengrad sich um mindestens 3 bis 4 Grad vom Breitengrad Ihrer Schule unterscheidet.

Wozu diese Maßnahme? Weil eine Partnerschule, die sich zum Beispiel 4 Grad südlich von Ihrem Wohnort befindet, einen Winkel messen wird, der um 4 Grad kleiner ist als derjenige, den Sie an diesem Tag messen werden. Leider sind die mit Ihren Schülern gemachten Messungen nicht beliebig genau. Sie werden es schon vermutet haben: Die Messwerte haben natürlich eine gewisse Fehler­breite. Sie werden einen Winkel messen, der entweder größer oder kleiner ist als der tatsächliche. Diese Fehlerbreite, also die Abweichung vom realen Wert hängt sowohl von der Qualität Ihres Gnomons ab (Länge und Rechtwinkligkeit des Stabs) als auch von seiner Aufstellung (Ist das Brett auch waagerecht? Wie genau ist der örtliche Längengrad eingezeichnet?). Das Ziel ist es, eine möglichst genaue Messung durchzuführen.

Wenn Sie bei jeder Messung einen Fehler von 3 bis 4 Grad machen, ist ganz klar, dass Ihre Berechnung des Erdumfangs stark vom tatsächlichen Wert ab­weichen wird, da der Fehler genau der Differenz zwischen Ihrer Messung und derjenigen Ihres Partners entspricht. Wenn Sie eine Messung machen, die auf plus minus 2 Grad genau ist, ist das schon besser, aber wenn der Fehler bei Ihrem Partner von ähnlicher Größenordnung ist, besteht immer noch die Gefahr, dass die Differenz der beiden Werte Null beträgt. Es ist also sehr wichtig, dass Ihr Gnomon gut justiert und positioniert ist, so dass Ihre Messungen auf (min­destens) 1 Grad genau sind.

Diese technische Anleitung soll Ihnen dabei helfen, Ihr Instrument zu überprü­fen und zu verbessern, damit Sie Ihren Partnern möglichst schnell sehr präzise Messungen übermitteln können. Es haben schon viele Schulen vor Ihnen ge­schafft, die Kriterien für solche präzisen Messungen zu erfüllen. Sie können es also auch schaffen! Wir haben in dieser Anleitung einige Ratschläge und Ideen zusammengestellt. Es sind natürlich nur Vorschläge und die Liste ist auch si­cherlich nicht vollständig. Zögern Sie also nicht, Ihre Partnerschulen innerhalb der Gruppe per E-Mail zu kontaktieren, um technische Tricks auszutauschen – dazu sind die Mailinglisten da!

Fehler, die sich aufsummieren!

Jedes Mal, wenn Sie zwei Teile Ihres Messinstruments zusammenfügen oder für eine Messung aufstellen, machen Sie unweigerlich kleine Fehler, die alle zusam­mengenommen Ihre Messung verfälschen können. Manchmal heben sich diese Fehler zufälligerweise auf, aber es kann genau so gut sein, dass sie sich sum­mieren, was für Ihre Messwerte natürlich sehr schlecht ist. Es ist also ratsam, dass Sie jeden Schritt mit der größtmöglichen Sorgfalt überprüfen.

Stellen Sie doch mit Ihren Schülern eine Liste der verschiedenen Schritte zu­sammen, vom Aufbau des Gnomons bis zur Messung: Auswahl und Länge des Stabs; Befestigung des Stabs senkrecht zum Brett, das selbst absolut eben sein sollte; Aufstellen des Bretts; überprüfen, dass das Brett waagerecht ist; den örtlichen Längengrad einzeichnen; beobachten, wann der Schatten des Stabs den Längengrad überquert; Messung der Länge dieses Schattens; gra­fische Darstellung des Winkels mit Hilfe der Längen des Stabs und des Schat­tens; Bestimmung des Winkels.

Sie müssen sich jetzt eingestehen, dass Sie bei jedem dieser Schritte einen kleinen Fehler machen. Sie werden daher verstehen, dass die letztendliche Messung und die daraus resultierende Berechnung des Erdumfangs stark von dem Wert, den Sie in Büchern nachschlagen können, abweichen kann! Kommen wir jetzt also zu einigen Tricks und Ideen, wie man diese Fehler abschätzen und minimieren kann.

Grundregel

Wie kann man den Fehler bei der Messung eines Winkels möglichst klein hal­ten? Indem beide Längen, die Sie einzeichnen um diesen Winkel zu bestimmen, so lang wie möglich sind (siehe Abb. 1). Man kann nie den genauen Wert einer Länge kennen, aber man kann sie mit einer gewissen Genauigkeit messen. Bit­ten Sie drei Schüler mit Hilfe eines 20 cm langen Lineals Ihren Schreibtisch auf einen halben Millimeter genau zu messen: Sie werden mit Sicherheit drei ver­schiedene Werte herausbekommen!

Nehmen wir jetzt einmal an, dass Sie den Winkel α auf der folgenden Abbildung messen wollen. Sie kennen die Längen A und B. Nehmen wir weiterhin an, dass diese Längen auf ±1 mm genau gemessen wurden (das ist ein realistischer Fehler). In der Abbildung kann man sehen, dass diese Ungenauigkeiten der Längen A und B eine Ungenauigkeit für den Wert des Winkels α nach sich ziehen.

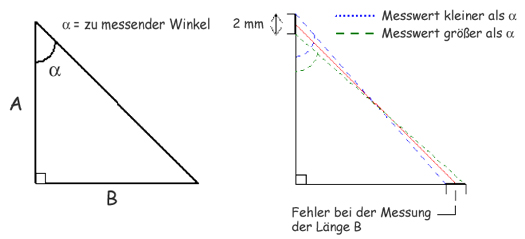
Abb. 1: Fehler bei den Längenmessungen führen zu Fehlern bei der Winkelbestimmung.

Um diese Ungenauigkeit zu reduzieren, verdreifachen oder vervierfachen Sie die Längen A und B. Die Messgenauigkeit der Längen bleibt dagegen gleich, da sie nur von Ihrer Art zu messen abhängt (Qualität Ihres Lineals und Ihres Ab­lesens). Die Ungenauigkeit für den Wert des Winkels wird kleiner. Abb. 2 sollte Sie davon überzeugen: Achten Sie auf die beiden extremen Winkel, die aus dieser Ungenauigkeit resultieren, sie entsprechen den Grenzen, zwischen denen der reale Wert des Winkels α liegt: in diesem Fall 45 Grad. Dieses Inter­vall wird auf der größten Abbildung deutlich kleiner (überprüfen Sie das mit Ihrem Geodreieck!)

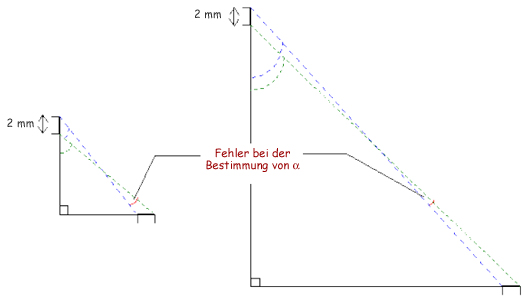
Abb. 2: Bei gleicher Messgenauigkeit wird der Fehler kleiner, wenn man größere Längen misst.

Für die Bestimmung des Winkels ist es also von Vorteil mit großen Längen zu hantieren.

Anwendungen

Verwenden Sie möglichst große Messinstrumente, zum Beispiel ein möglichst großes Geodreieck, um zu überprüfen, ob Ihr Gnomon auch tatsächlich senk­recht zum Brett angebracht ist.

Achtung: Die Rechtwinkligkeit muss in zwei zueinander senkrechten Richtungen überprüft werden. Es kann nämlich passieren, dass der Gnomon in einer belie­bigen Richtung geneigt ist!

Ein längerer Gnomon ist leichter senkrecht zum Brett zu befestigen. Wenn er allerdings länger als 20 cm ist, wird sein Schatten an der Spitze schnell un­scharf, auch zum Sonnenmittag. Am besten ist ein Gnomon, der ca. 10 cm lang ist. Wenn Sie eine Wasserwaage gebaut haben, um zu überprüfen, ob das Brett auch waagerecht ist, wird diese Wasserwaage um so präziser sein, je größer die Oberfläche der Flüssigkeit ist (aus dem gleichen Grund, der oben für die Messung eines Winkels aufgeführt wurde). Benutzen Sie möglichst feine Bleistifte, um die Striche zu zeichnen, deren Längen gemessen werden sollen, so reduzieren Sie den Fehler bei der Bestimmung des Winkels. Verwenden Sie auch möglichst große Geodreiecke (oder Winkelmesser), um den Winkel abzu­lesen, dadurch wird Ihr Wert genauer.

Bemerkung: Je nach Form Ihres Gnomons (mit spitzem oder flachem Ende) müssen Sie die Schattenlänge von unterschiedlichen Punkten am Fuß des Gnomons aus messen; beobachten Sie dazu genau die folgende Abbildung, da ansonsten Ihre Messungen womöglich mit einem systematischen Fehler behaf­tet sein werden.

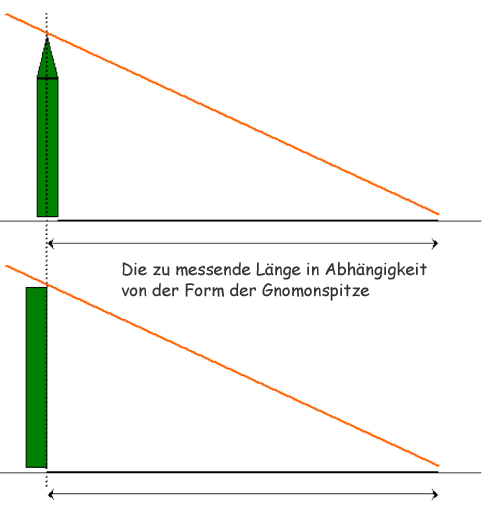
Abb. 3: Bei unterschiedlichen Formen der Spitze des Gnomons müssen die Längen der Schatten entsprechend anders gemessen werden.

Schätzen Sie selber Ihre Genauigkeit ein!

Sie können ganz einfach selbst Ihre Genauigkeit abschätzen: Sie brauchen nur jeden Tag Messungen durchzuführen. Von einem Tag zum nächsten verändert sich der Winkel zwischen Sonne und Vertikale nur sehr wenig, zwischen 0,1 und 0,2 Grad pro Tag ab Mitte Mai. Das ist zu wenig, um von Ihnen gemessen zu werden. Wenn Sie also den Winkel drei Tage hintereinander messen, bekom­men Sie ein Gefühl dafür, welche (zufallsbedingten) Fehler Sie während der Einstellung Ihres Gnomons und der Messung machen. Ihre drei Messwerte soll­ten so nah wie möglich beieinander liegen. Sie werden dadurch allerdings nicht die genaue Abweichung Ihres Messwerts vom wirklichen Wert des Winkels herausbekommen. Machen Sie sich jedoch keine Sorgen, wir verfolgen Ihre ge­samten Ergebnisse engmaschig und werden Ihnen – falls es für die Interpre­tation Ihrer Ergebnisse notwendig sein sollte – die tatsächliche Genauigkeit Ihrer Messungen mitteilen.

Viel Erfolg, Sie haben Ihr Ziel fast erreicht!

Ergänzung

Hier ist die Beschreibung eines von Alain Rouquet und seiner Klasse hergestell­ten Gnomons. Mit diesem sehr einfachen Gnomon konnten exzellente Ergeb­nisse erzielt werden!

"An der Herstellung dieses Gnomons ist nichts besonders originell: ein Tablett aus Melamin, das auf einen Tisch gestellt wird, auf einer Kante des Tabletts ein Holzstab (Durchmesser: 8 mm), dessen Länge so gewählt ist, dass sich die Holzstabspitze 10 cm über der Tischplatte befindet, der Stab ist mit einer Rohrschelle (Klempnerbedarf) befestigt (die Schraube sollte nicht zu stark angezogen sein, damit die Kinder den Stab jederzeit nachjustieren können).

Bei jeder Messung überprüft ein Kind, dass das Tablett auch waagerecht ist und der Gnomon senkrecht dazu, ein anderes Kind markiert auf das Tablett das Ende des Schattens. Zurück im Klassenraum wird eine weitere Gruppe aktiv, sie zeichnet das berühmte Dreieck und misst den Winkel des Tages. Eine letzte Gruppe geht dann ganz aufgeregt zum Computer und trägt dort auf der Web­seite des Projektes den Wert für den Winkel des Tages ein.

Die Methode des direkten Anvisierens ist etwas enttäuschend. Es ist schwer, genaue Messwerte zu erhalten. Dafür lieben es die Kinder, die Sonne mit den Sonnenfinsternisbrillen anzuschauen."

© Sonnentaler/La main à la pâte | Impressum | Disclaimer | Datenschutz | RSS | E-Mail

© Sonnentaler / La main à la pâte  http://www.sonnentaler.net/