Messung des Winkels der Sonnenstrahlen mit einem Quadranten (fakultativ)
| Publikation: | 27.10.2007 |
| Lernstufe: | 3 |
| Material: |
|
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Im Folgenden wird ein anderes Verfahren für die rasche und einfache Messung des Winkels der Sonnenstrahlen beschrieben, das Ihre Schüler – neben der Methode mit dem Eratosthenes-Gnomon – mit größtem Vergnügen anwenden werden. Angelehnt an das Prinzip des direkten Anvisierens mit einem Sextanten in der Schifffahrt, kann man mit einem so genannten Quadranten den Winkel der Sonnenstrahlen (den wir mit α [alpha] bezeichnen) auch direkt bestimmen, ohne einen Gnomon zu benutzen. Die nachstehende Abbildung veranschaulicht das Prinzip. Es sei jedoch bereits jetzt darauf hingewiesen, dass beim Anvisieren niemals direkt in die Sonne geschaut werden darf. Man nimmt stattdessen die Projektion der Sonne (die durch ein Papierrohr scheint) auf einen Schirm (Blatt Papier) zur Hilfe.
Und noch einmal: Wenn die Augen nicht durch Spezialfilter geschützt sind, sollte man auf keinen Fall direkt in die Sonne gucken.
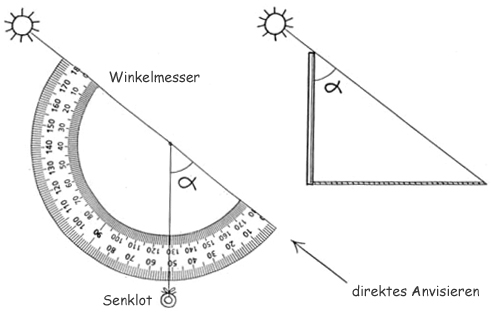
Abb. 5: Funktionsprinzip des Quadranten im Vergleich zur Messung mit einem Gnomon
Anfertigung eines Quadranten für die gesamte Klasse
Der Quadrant muss wie der Eratosthenes-Gnomon mit besonderer Sorgfalt angefertigt werden, um den Winkel sehr genau (theoretisch bis auf ein Viertelgrad) messen zu können. Die nachstehende Abbildung und einige ergänzende Erläuterungen zeigen, wie man vorgehen muss.
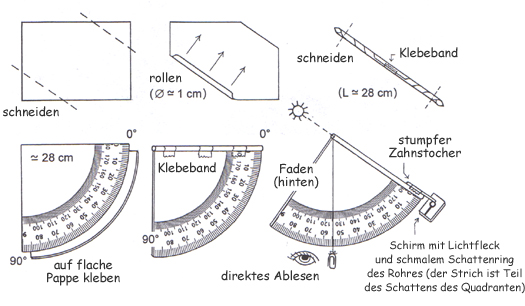
Abb. 6: Bau eines Quadranten
Achtet beim Einrollen des Blattes darauf, dass das Rohr schön gleichmäßig zylindrisch ist. Fotokopiert und vergrößert den für die Messung benötigten Teil eines Winkelmessers in zwei Stufen, beim zweiten Mal auf ein DIN A3-Blatt. Vergewissert Euch, dass der rechte Winkel bei der größten Vergrößerung immer noch 90° beträgt, da manche Kopierer verzerren. Das Senklot darf nur wenig über den Quadranten hinausreichen, damit es (durch wiederholte leichte Berührungen mit dem Quadranten) schnell zur Ruhe kommt.
Bei dem Schirm handelt es sich lediglich um ein kleines Stück Papier, auf dem ein runder Lichtfleck – die Projektion der Sonne durch das Papierrohr – beobachtet werden soll; eine Größe von 2 cm×2 cm reicht also völlig aus. Der Schirm wird mit Hilfe des Zahnstochers fest mit dem Rohr verbunden: Das eine Ende des Zahnstochers wird mit Klebeband an das Rohr befestigt, das andere Ende mittig durch das Stück Papier gestochen, so dass letzteres senkrecht zum Rohr ist. Der Abstand zwischen Schirm und Rohr sollte ungefähr 2 cm betragen, so dass man von der Seite noch auf den Schirm blicken kann, der Sonnenfleck auf dem Schirm aber möglichst kreisrund und scharf ist.
Vorsicht! Der Quadrant ist etwas windempfindlich. Verwendet ihn an einem windgeschützten Ort oder verzichtet lieber auf diese Messmethode. Auf jeden Fall muss der mit dem Quadranten gemessene Wert jedes Mal mit dem von einem anderen Kind mit dem Gnomon ermittelten Wert verglichen werden.
Ablesen des Winkels auf dem Quadranten
Einige Minuten vor dem Sonnenmittag stellt sich der mit der Messung betraute Schüler in die Sonne und versucht, die Sonne durch das Rohr scheinen zu lassen, ohne zunächst auf das Lot zu achten. Dazu muss er versuchen, den Schatten des Rohres "verschwinden" zu lassen. Wenn er das geschafft hat, ist auf dem Schirm ein heller runder Lichtfleck zu sehen: die Projektion der Sonne durch das Rohr. Um den Lichtfleck herum sieht man einen schmalen kreisrunden Ring – den Schatten der Rohrwand –, von dem ein Strich bis zum Papierrand geht – ein Teil des Schattens des (Profils des) Quadranten.
Sobald auf dem Schirm der runde Lichtfleck mit seinem dunklen Ring zu sehen ist, schaut er auf den Faden: Hängt er zu weit vom Quadranten weg oder liegt er zu stark auf ihm auf?
In beiden Fällen muss die Position des Instruments korrigiert werden: Der Faden sollte den Quadranten nur leicht berühren. Beim Korrigieren der Position kann es nun allerdings passieren, dass der Lichtfleck auf dem Schirm wieder verschwindet. Wenn man den Faden des Senklots als senkrechte Achse betrachtet, um die sich das Instrument drehen lässt, kann man dessen Ausrichtung vorsichtig korrigieren, bis der Lichtfleck wieder sichtbar wird.
Zum Zeitpunkt des Sonnenmittags, bei eingependeltem Senklot und nach einem kurzen letzten Blick auf den Lichtfleck mit seiner kreisrunden Begrenzung, liest der Schüler auf ein Viertelgrad genau die Größe des Winkels auf der Skala ab. Der ganze Vorgang dauert nur ein bis zwei Minuten. Das Ergebnis wird natürlich mit dem Messwert verglichen, der zum gleichen Zeitpunkt mit dem Gnomon ermittelt wurde.
Letzte Aktualisierung: 29.11.2023






