Wie misst man einen Winkel?
| Publikation: | 30.4.2008 |
| Lernstufe: | 3 |
| Dauer: | 1 Stunde, im Klassenraum, entweder mit der ganzen Klasse oder in kleinen Gruppen |
| Material: |
Für jede Gruppe von 3-5 Schülern:
|
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Valérie Munier vom Physik-Didaktiklabor der Universität Paris 7 zu den Schwierigkeiten, die den Schülern der Begriff Winkel bereitet
In dieser Projektphase sollen sich die Schüler mit dem Begriff des Winkels befassen. Für viele ist ein Winkel ein Gebilde aus zwei gleichlangen Geraden, deren Endpunkte sich in einem Punkt treffen. Schon wenn zwei Abbildungen sich lediglich dadurch unterscheiden, dass eine der Geraden etwas länger ist, haben sie den Eindruck, dass es sich um zwei verschiedene Winkel handeln würde. Man sollte daher betonen, dass ein Winkel als die Öffnung zwischen zwei Geraden definiert ist, wobei diese Geraden beliebig lang sein können (und sich sogar auch schneiden) können.
Wie man diese Schwierigkeiten überwinden kann
Verteilen Sie Fotokopien, auf denen mehrere Paare von gleichen Winkeln abgebildet sind, bei denen die den Winkel bildenden Geraden (Schenkel) aber unterschiedlich lang sind. Wenn die Kinder diese Winkel ausschneiden und aufeinander legen, werden sie sehen, dass die Öffnung zwischen beiden Geraden, also der Winkel bei jedem Paar trotzdem gleich ist.
Sie können die Kinder auch verschiedene Winkel ordnen lassen, z. B. vom spitzesten bis zum stumpfesten (vom kleinsten bis zum größten). Dazu schneiden sie aus Tonpapier Dreiecke aus und markieren mit einem kleinen Bogen, welcher Winkel des Dreicks betrachtet werden soll. Durch Übereinanderlegen der ausgeschnittenen Dreiecke können sie die verschiedenen Winkel vergleichen (wobei sie darauf achten sollten, dass die Scheitelpunkte der Winkel übereinander liegen).
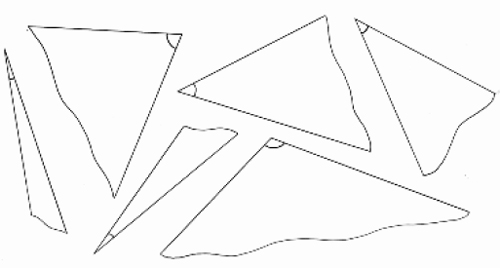
Abb. 1: Verschiedene Winkel, die die Schüler ausschneiden und vergleichen können
Sie können sich auch im Klassenraum nach allen möglichen Winkeln umschauen. Aber sie werden feststellen, dass die meisten Winkel gleich sind: Bücher, Hefte, Möbel, Wände, Fenster usw. bilden alle rechte Winkel. Auch das ist wieder ein Beweis, dass der Wert des Winkels nichts mit der Länge seiner Schenkel zu tun hat.
Besprechung
Die Kinder zerbrechen sich den Kopf über das Ende des historischen Textes: Wie ist Eratosthenes wohl auf den Wert für den Winkel gekommen? Schlagen Sie ihnen vor, den Obelisken und seinen Schatten auf kariertes oder Millimeterpapier zu zeichnen. Legen Sie gemeinsam den Verkleinerungsmaßstab fest.
Nun wird sicher die folgende Frage aufkommen: Kann man sicher sein, dass die Neigung der Sonnenstrahlen in dieser verkleinerten Darstellung die gleiche ist wie in natura? Mit anderen Worten: Bleibt der Winkel zwischen den Strahlen und dem Obelisken gleich, wenn man den Maßstab ändert, oder wird er in gleichem Maße verkleinert?
Die Kinder diskutieren über diese Frage, die sie auch ganz konkret formulieren können: "Wirft ein doppelt so hoher Gnomon (zur gleichen Zeit) einen doppelt so langen Schatten? Und verdoppelt sich dabei der Winkel?" (Die Antwort auf die erste Frage lautet natürlich Ja, diejenige auf die zweite Nein). Die Schüler notieren ihre Vermutung in ihr Versuchsheft. Sie wird wahrscheinlich lauten: "Ja, der Schatten wird bestimmt doppelt so groß sein". Sie können dies auf dem Papier überprüfen (siehe weiter unten) und natürlich auch im Freien. Bei der Suche nach Antworten auf die obigen Fragen kann man ganz nebenbei den Begriff Verhältnis einführen.
An einer Zeichung den Winkel der Sonnenstrahlen verdeutlichen
Die Kinder ziehen zunächst mit dem Lineal eine waagerechte Gerade auf ihr kariertes Blatt: Diese soll den Boden darstellen. Anschließend wählen sie die Neigung der Sonnenstrahlen (siehe Abb. 2) und zeichnen mit dem Lineal lauter parallele Strahlen. Danach malen sie einen etwa 6 cm hohen Gnomon (oder schneiden ihn aus buntem Papier aus), der auf dem "Boden" steht und dessen Spitze einen der Strahlen berührt.
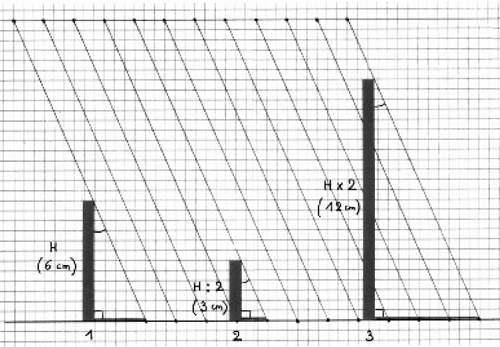
Abb. 2: Der Winkel zwischen Sonnenstrahlen und Gnomon ist unabhängig von der Höhe des Gnomons.
Sie erhalten so ein rechtwinkliges Dreieck, da der Gnomon und der Boden einen rechten Winkel bilden. Die Länge des Schattens wird von dem die Spitze des Gnomons streifenden und auf den Boden treffenden Strahl bestimmt. Die Kinder zeichnen mit einem dicken Strich den Schatten und notieren sorgfältig seine Länge. Dann zeichnen oder legen sie einen halb so großen (3 cm) und einen doppelt so großen (12 cm) Gnomon auf das Papier und messen jeweils dessen Schattenlänge. Indem sie jedes Mal das Verhältnis zur Schattenlänge des ersten Gnomons bilden, erhalten sie für den zweiten Schatten die Hälfte und für den dritten das Doppelte der Länge des ersten Schattens, womit sich ihre Vermutung bestätigt findet.
Eine grundlegende Entdeckung
Und wie steht es mit dem Einfallswinkel der Sonnenstrahlen? Hat er sich von einem Gnomon zum anderen verändert? "Es sieht so aus, als wäre der Winkel gleich geblieben". Nach Überprüfung mit Hilfe von Pauspapier erweist sich dies als richtig. Doch was geschähe, wenn man den Versuch mit einem drei- oder fünfmal größeren oder kleineren Gnomon machen würde? Die Antwort ist einhellig: "Die Schatten wären drei- oder fünfmal länger oder kürzer, aber der Winkel würde gleich bleiben."
Und was würde passieren, wenn man eine neue Zeichnung mit einer anderen Neigung der Sonnenstrahlen machen würde? Die Schüler werden feststellen, dass dies an den vorhergehenden Schlussfolgerungen nichts ändert, weil die auf die Gnomone treffenden Sonnenstrahlen parallel sind. Was für eine Entdeckung! Ganz gleich, wie hoch ein Gnomon ist, der Winkel der Sonnenstrahlen zu einem gegebenen Zeitpunkt ist immer gleich. Der Obelisk des Eratosthenes hätte also höher oder niedriger sein können, Eratosthenes hätte in jedem Fall den gleichen Winkel gemessen.
Schlussfolgerung: Man kann den Verkleinerungsmaßstab für die Darstellung des Obelisken von Alexandria und seines Schattens beliebig wählen, denn die Größe des Winkels bleibt gleich. Jetzt geht es also nur noch darum, auf dem Papier den Winkel der Sonnenstrahlen zu messen.
Wie verwendet man einen Winkelmesser?
Sollten Ihre Schüler noch nicht mit einem Winkelmesser umgehen können, so ist das kein Problem. Sie können sich auf sehr einfache Weise mit diesem Messinstrument vertraut machen.
Geben Sie Ihnen mehr oder weniger stark vergrößerte Fotokopien von einem Winkelmesser aus Plexiglas und verschiedene auf Pauspapier gezeichnete Winkel. Nachdem die Schüler erkannt haben, dass sich der Scheitelpunkt des Winkels mit dem kleinen Loch in der Mitte des Winkelmessers und einer der beiden Schenkel sich mit dem Nullgradstrich eines der beiden in Grade unterteilten Bögen decken muss, üben sie sich im Messen der ihnen vorgelegten Winkel. Machen Sie sie darauf aufmerksam, dass die Messung umso genauer wird, je größer der Radius des in Grade unterteilten Bogens auf der Fotokopie ist, und dass es somit angebracht ist, sehr stark vergrößerte Fotokopien zu verwenden.
Letzte Aktualisierung: 29.11.2023






