Unterrichtsstunde 5.1: Wohnung oder Einfamilienhaus – macht das einen Unterschied?
| Autoren: | |
| Publikation: | 12.4.2011 |
| Lernstufe: | 3 |
| Ziele: |
|
| Angestrebte Kenntnisse: |
|
| Schwerpunkt: | Mathematik |
| Wortschatz: | Wohnfläche, Grundfläche, Volumen, Trennwand |
| Dauer: | 1 Stunde 15 Minuten |
| Material: |
Für jede Gruppe:
|
| Herkunft: | La main à la pâte, Paris |
Einstiegsfrage
Zu Beginn der Unterrichtsstunde wird kurz herumgefragt, wie die Schüler wohnen. Wohnen sie größtenteils in Einfamilienhäusern oder in Häusern mit mehreren Wohneinheiten? Der Lehrer fordert die Kinder auf, sich in die Rolle von Stadtplanern oder Stadtbaumeistern zu versetzen, die dem Zuzug von neuen Bewohnern gerecht werden müssen.
Es werden zwölf Würfel, die jeweils eine Wohnung für eine Familie symbolisieren, an jede Schülergruppe verteilt. Der Arbeitsauftrag lautet: "Findet drei verschiedene Lösungen zur Verteilung dieser zwölf Wohneinheiten auf einem Baugrund". Es sollte bedacht werden, dass jede Wohnung wenigstens eine Seite (das heißt eine Außenmauer) mit "freiem Ausblick" hat. Ein Würfel, der von allen Seiten durch andere umstellt ist, entspräche einer fensterlosen Wohnung.
Pädagogische Anmerkungen
- Betonen, dass ein Würfel eine Wohnung darstellt und nicht etwa ein Zimmer.
- Alle Würfel müssen eingesetzt werden!
- Es müssen unbedingt Würfel sein und keine Quader, weil die anschließenden Berechnungen davon ausgehen, dass alle Flächen gleich groß sind.
Untersuchung mit Experiment
Der Lehrer verteilt das Arbeitsblatt 16, mit dessen Hilfe die Aufbauten miteinander verglichen werden sollen. Er erläutert anhand einiger Beispiele, wie man die Flächen zählt, und weist besonders auf die Trennwände und Trenndecken hin. Er zeigt mit zwei aneinanderklebenden Würfeln, dass dort, wo zwei Wohneinheiten aneinandergrenzen, nur eine gemeinsame Wand ist (oder eine gemeinsame Decke).
Bei der Anordnung der 12 Wohneinheiten kommen die Schülergruppen zu ganz unterschiedlichen Lösungen. Zum Beispiel:
- 12 einzeln aufgestellte Würfel: Einzelhäuser, zwischen denen ein Garten liegt, eine Straße vorbeiführt, ...;
- 12 "ebenerdig" aneinandergereihte Würfel: Reihenhäuser;
- 2 Stockwerke zu je 6 Würfeln;
- 3 Stockwerke zu je 4 Würfeln;
- Eine Mischung von Einzelhäusern und Apartmentbauten verschiedener Größe und Form, ...
Da die Formen frei gewählt werden können, werden mehr oder weniger kompakte oder bizarre Anordnungen herauskommen. Der Lehrer muss prüfen, ob in jeder Gruppe die Flächen richtig gezählt wurden, vor allem die Zwischenflächen.
Gemeinsame Erörterung
Nacheinander präsentiert jeweils ein Mitglied jeder Gruppe eine Lösung (die sich von denen der anderen Gruppe unterscheidet), die zum Beispiel mit Patafix an der Tafel befestigt wird.

Abb. 1: Zwölf Würfel – unterschiedlich gestapelt
Pädagogische Anmerkung
Wenn möglich sollten Würfel verwendet werden, die aneinander haften, damit die Konstruktion auch an der Tafel hält. Falls solche nicht verfügbar sind, kann man die Anordnungen zur Not auch auf einen Tisch stellen oder Fotos machen, die man wiederum an die Tafel befestigt.
Die Zählung der Grundflächen und der Zwischenflächen wird überprüft, ebenso die Gesamtzahl der Flächen. Der Lehrer kann anschließend fragen: "Was meint ihr: Welches sind die umweltfreundlichsten Anordnungen? Und warum?" Da die Frage nicht einfach ist, können zusätzliche Hinweise gegeben werden: "Welche Ähnlichkeiten und Unterschiede stellt ihr fest? Was könnte man zählen? Was haben wir bereits gelernt, was uns jetzt helfen könnte?"
Der Lehrer betont die Tatsache, dass der Wohnraum in allen Anordnungen der gleiche ist: Jede Familie hat gleich viel Platz in der Wohnung. Die Schüler begreifen, dass kleine Grundflächen günstiger sind, weil der Baugrund in der Stadt begrenzt ist.
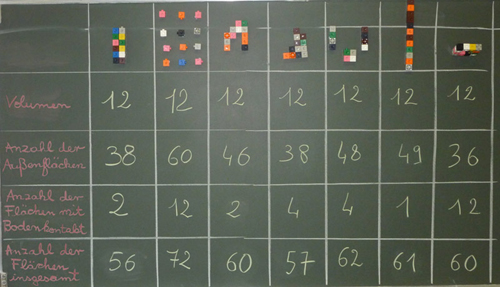
Abb. 2: Volumen, Anzahl der Außenflächen, der Flächen, die Bodenkontakt haben, und der Flächen insgesamt – je nach Anordnung der Würfel
Wissenschaftliche Anmerkung
Hier stimmen ökonomische und ökologische Überlegungen überein: Die Ausdehnung der Städte ist für die Umwelt eine Katastrophe!
Aus der Gesamtzahl der Mauern lässt sich auf die Gesamtmenge an Baumaterial schließen: Je mehr Mauern, desto mehr Material. Man wird also versuchen hier zu sparen (in der Unterrichtsstunde 2.2: Der Lebenszyklus von Baustoffen haben die Schüler bereits die Auswirkung von Baumaterialien wie Beton auf die Umwelt erkundet). Das bedeutet, dass man eher Mehrfamilienhäuser bauen sollte. Ein letzter Aspekt, auf den die Kinder nicht ohne Weiteres kommen, ist die Größe der Außenflächen. Der Lehrer kann sie auf ihre eigene Erfahrung hinweisen: "Was meint ihr, was ist leichter zu heizen, eine Wohnung oder ein Haus?" Eine Wohnung muss weniger geheizt werden als ein Haus, weil die Nachbarwohnungen wie eine Wärmedämmung wirken. Im Winter, wenn es kalt ist, sind kleinere Außenflächen besser.
Pädagogische Anmerkung
Den Schülern ist der Zusammenhang zwischen der Größe der Außenfläche und der Geschwindigkeit des Wärmeaustauschs an Außenflächen nicht unbedingt klar. Es handelt sich eher um eine Intuition als um erworbenes Wissen. Daher wollen wir in der nächsten Unterrichtsstunde diesen Zusammenhang mit einem sehr einfachen Experiment aufklären.
Zusammenfassung
Der Lehrer fordert die Schüler auf, jeder für sich im Arbeitsheft eine Zusammenfassung zu formulieren, als Antwort auf die Frage "Wohnung oder Haus – macht das einen Unterschied?" Einige Schüler lesen der Klasse vor, was sie geschrieben haben. Daraus entsteht eine gemeinsame Formulierung. Etwa:
"Kollektives Wohnen ist wirtschaftlicher und umweltfreundlicher als das Wohnen in Einfamilienhäusern. Außerdem spart man Baugrund, Energie und Baumaterial."
Letzte Aktualisierung: 29.11.2023






